|
“与抛物线的轴平行的直线和抛物线只有一个交点”(第98页练习第3题)。这样的直线是否抛物线的切线?为什么? 不是。与圆有且只有一个交点的直线,称为圆的切线。这一定只适合于圆。当然也可以扩大到椭圆与其他一些曲线,但不适合于双曲线和抛物线。例如,x轴与抛物线y2=2px (p>0)显然有且只有一个交点,但对于这条抛物线来说,只有y轴是它的切线,x轴不是它的切线。又如,在高等数学中可以证明,平行于双曲线的渐近线的直线与双曲线有且只有一个交点,但它不是双曲线的切线。 在高等数学中,曲线在某一点处的切线是这样定义的:如图,已知P点是曲线C的某一点,l是经过点P的一条割线,与C相交于点Q1,让l1绕着P旋转到l2的位置,l2与C点相交于点Q2,将这一绕点P旋转的过程继续下去,得到一系列割线l1,l2…,它们与C的交点Q1,Q2…逐步向点P靠近。那么,我们把这一系列割线的极限位置叫做曲线C在点P处的切线。 至于对直线与圆锥曲线的位置关系问题的处理,仍然是: 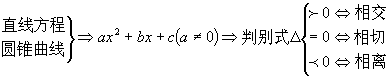 (责任编辑:admin) |
