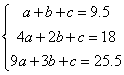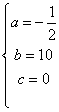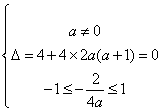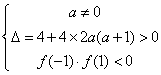西城教育研修学院中学数学室供稿
(试卷满分为150分,考试时间为120分钟)
试卷分为两卷,卷(I)100分,卷(II)50分
卷(I)
一.选择题:本大题共10小题,每小题5分,共50分
1.集合{1,2,3}的真子集的个数为( )
A.5 B.6 C.7 D.8
2.函数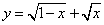 的定义域为( ) 的定义域为( )
A. B. B.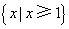 C. C.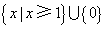 D. D.
3.函数 ,则 ,则 ( ) ( )
A. B. B.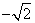 C. C.  D. D. 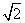
4.设全集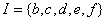 ,若 ,若 , ,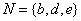 ,则 ,则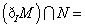 ( ) ( )
A.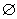 B. B.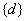 C. C.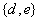 D. D.
5.下列函数中的值域是 的是( ) 的是( )
A.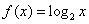 B. B.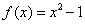 C. C.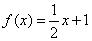 D. D.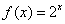
6.下列函数中,在区间 上为增函数的是( ) 上为增函数的是( )
A.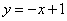 B. B.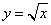 C. C.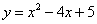 D. D.
7.函数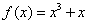 的图象关于( ) 的图象关于( )
A.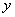 轴对称 B. 直线 轴对称 B. 直线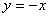 对称 对称
C. 坐标原点对称 D. 直线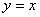 对称 对称
8.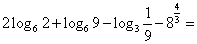 ( ) ( )
A.12 B. C. C. D. D.
9.函数 的图象是下列图象中的( ) 的图象是下列图象中的( )
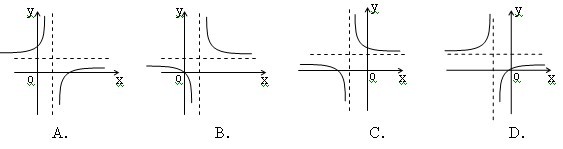
10.设 且 且 ,则( ) ,则( )
A.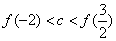 B. B.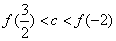
C.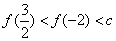 D. D.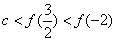
二.填空题:本大题共4小题,每小题5分,共20分
11.若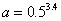 、 、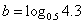 、 、 ,则 ,则 的大小关系是____________。 的大小关系是____________。
12.若函数 满足 满足 ,则 ,则 ____________。 ____________。
13.已知:集合 , ,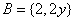 ,若 ,若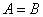 ,则 ,则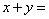 ____________。 ____________。
14.函数 的定义域是___________,单调减区间是__________。 的定义域是___________,单调减区间是__________。
答 题 纸
班级 姓名 成绩
一.选择题(本大题共10小题,每小题5分,共50分)
题号
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
答案
|
|
|
|
|
|
|
|
|
|
|
二.填空题(本大题共4小题,每小题5分,共20分)
三.解答题(本大题共3小题,每小题10分,共30分)
15.已知:函数 的定义域为 的定义域为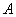 ,集合 ,集合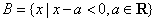 , ,
(1)求:集合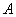 ; ;
(2)求: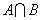 。 。
16.某厂今年1月、2月、3月生产某种产品分别为9.5万件、18万件、25.5万件。如果该厂每月生产此种产品的产量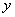 与月份 与月份 之间满足二次函数关系: 之间满足二次函数关系: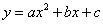 , ,
(1)求:此二次函数的解析式;
(2)求:哪个月份的产量最大,最大产量是多少?
17.已知:函数 , ,
(1)求:函数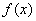 的定义域; 的定义域;
(2)判断函数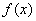 的奇偶性并说明理由; 的奇偶性并说明理由;
(3)判断函数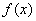 在 在 上的单调性,并用定义加以证明。 上的单调性,并用定义加以证明。
卷(Ⅱ)
一.选择题:本大题共3小题,每小题4分,共12分
1.函数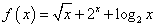 中,若 中,若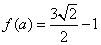 ,则 ,则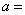 ( ) ( )
A.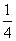 B. B.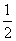 C. C.  D. D.
2.如果函数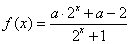 是奇函数,那么 是奇函数,那么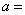 ( ) ( )
A.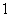 B. B. C. C. D. D.
3.设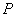 、 、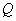 为两个非空实数集,定义集合 为两个非空实数集,定义集合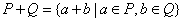 .若 .若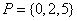 , , 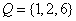 ,则 ,则 中元素的个数是( ) 中元素的个数是( )
A.6 B.7 C.8 D.9
二.填空题:本大题共2小题,每小题4分,共8分
4. = 。 = 。
5.如果函数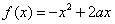 在区间[1,2]上是减函数,那么实数 在区间[1,2]上是减函数,那么实数 的取值范围是 ;如果函数 的取值范围是 ;如果函数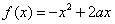 与函数 与函数 在区间[1,2]上都是减函数,那么实数 在区间[1,2]上都是减函数,那么实数 的取值范围是 。 的取值范围是 。
三.解答题:本大题共3小题,满分共30分
6.求:函数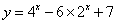 ( ( )的最值及取得最值时的 )的最值及取得最值时的 值。 值。
7.已知:函数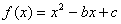 ,若 ,若 ,且 ,且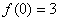 , ,
(1)求: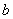 、 、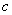 的值; 的值;
(2)试比较 与 与 ( (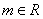 )的大小。 )的大小。
8.已知:函数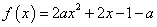 在区间 在区间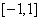 上有且只有一个零点, 上有且只有一个零点,
求:实数a的取值范围。
参考答案
卷(I)
C D A C D B C B A B
11.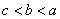 ; 12.6; 13.2或6; 14. ; 12.6; 13.2或6; 14. , ,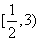 ; ;
15.解:(1) ,定义域 ,定义域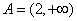 ;…………………………4分 ;…………………………4分
(2)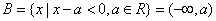 …………………………6分 …………………………6分
①当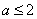 时, 时, ; …………………………8分 ; …………………………8分
②当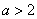 时, 时,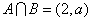 …………………………10分 …………………………10分
16.解:(1)由题知: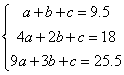  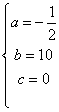  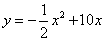 ……………6分 ……………6分
(2)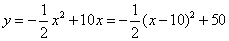 …………………………8分 …………………………8分
当 时, 时,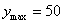 (万件),即:10月份的产量最大,最大产量为50万件。………10分 (万件),即:10月份的产量最大,最大产量为50万件。………10分
17.解:(1)定义域: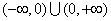 ; …………………………2分 ; …………………………2分
(2)定义域关于原点对称, , ,
则:函数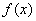 是奇函数; …………………………4分 是奇函数; …………………………4分
(3)判断:函数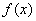 在 在 上是增函数, …………………………5分 上是增函数, …………………………5分
证明:任取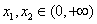 且 且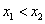 , ,
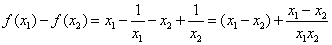 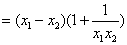 …………………7分 …………………7分
∵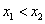 ,∴ ,∴ ,∵ ,∵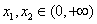 ,∴ ,∴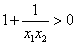 , ,
∴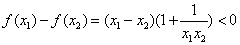 ,即: ,即: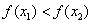 …………………………9分 …………………………9分
∴函数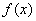 在 在 上是增函数。 …………………………10分 上是增函数。 …………………………10分
卷(II)
BAC 4.-4;5.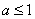 , ,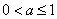 , ,
6.解:令 , , ,则: ,则: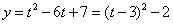 , …………………………4分 , …………………………4分
当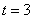 即: 即: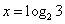 时, 时,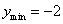 , …………………………6分 , …………………………6分
当 即: 即: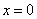 时, 时,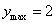 。 …………………………8分 。 …………………………8分
7. 解:(1)∵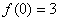 ,∴ ,∴ , …………………………1分 , …………………………1分
∵ ,∴ ,∴ 为图象的对称轴,∴ 为图象的对称轴,∴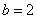 ,…………………………3分 ,…………………………3分
∴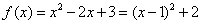 …………………………4分 …………………………4分
(2)当 时,∵ 时,∵ ,∴ ,∴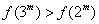 ; …………………………6分 ; …………………………6分
当 时,∵ 时,∵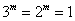 ,∴ ,∴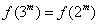 ; …………………………7分 ; …………………………7分
当 时,∵ 时,∵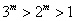 ,∴ ,∴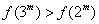 ; …………………………8分 ; …………………………8分
综上所述: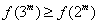 。 …………………………10分 。 …………………………10分
8.解:(1)当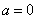 时, 时,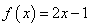 ,其零点为 ,其零点为 ; …………………………2分 ; …………………………2分
(2)当 ,二次函数只有一个零点且在 ,二次函数只有一个零点且在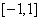 时,满足条件, 时,满足条件,
即: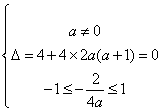  无解; …………………………5分 无解; …………………………5分
(3)当 ,二次函数有两个零点,一个在 ,二次函数有两个零点,一个在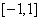 时,满足条件, 时,满足条件,
即: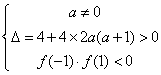  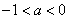 或 或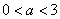 ; …………………………8分 ; …………………………8分
(4)当 是零点时, 是零点时,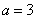 ,此时 ,此时 ,零点是: ,零点是: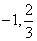 ,不合题意, ,不合题意,
当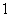 是零点时, 是零点时, ,此时 ,此时 ,零点是: ,零点是: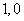 ,不合题意; ………11分 ,不合题意; ………11分
综上所述: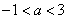 是满足题意。 …………………………12分 是满足题意。 …………………………12分
四中高一数学期中测试卷.zip
(责任编辑:admin) |