|
一、选择题 1.下列语言中,哪一个是输入语句( ) A.PRINT B.INPUT C.IF D.LET 参考答案:B 2.下列命题是真命题的是( ) ①必然事件的概率等于1 ②某事件的概率等于1.1 ③互斥事件一定是对立事件 ④对立事件一定是互斥事件 ⑤在适宜的条件下种下一粒种子,观察它是否发芽,这个试验为古典概型 A.①③ B.③⑤ C.①③⑤ D.①④⑤ 参考答案:D 3.有20位同学,编号从1至20,现在从中抽取4人作问卷调查,用系统抽样方法确定所抽的编号为( ) A.5,10,15,20 B.2,6,10,14 C.2,4,6,8 D.5,8,11,14 参考答案:A 4.x=5 y=6 PRINT xy=11 END 上面程序运行时输出的结果是( ) A.xy=11 B.11 C.xy=11 D.出错信息 参考答案:D 5.从分别写上数字1,2,3……9的9张卡片中,任意取出两张,观察上面的数字,则两数积是完全平方数的概率为( ) A. 参考答案:A 6.有一农场种植一种水稻在同一块稻田中连续8年的年平均产量如下:(单位:kg) 450 430 460 440 450 440 470 460 则其方差为( ) A.120 B.80 C.15 D.150 参考答案:D 7.在长为10 cm的线段AB上任取一点P,并以线段AP为边作正方形,这个正方形的面积介于25 cm2与49 cm2之间的概率为( ) A. 参考答案:B 8.“吸烟有害健康”,那么吸烟与健康之间存在什么关系( ) A.正相关 B.负相关 C.无相关 D.不确定 参考答案:B 9.二进制数111011001001 (2)对应的十进制数是( ) A.3901 B.3902 C.3785 D.3904 参考答案:C 10.在10枝铅笔中,有8枝正品和2枝次品,从中不放回地任取2枝,至少取到1枝次品的概率是( ) A. 解析:方法一(直接法):至少取到1枝次品包括:A=“第一次取到次品,第二次取到正品”;B=“第一次取到正品,第二次取到次品”;C=“第一、二次均取到次品”三种互斥事件,所以所求事件的概率为P(A)+P(B)+P(C)= 方法二(间接法):至少取到1枝次品的对立事件为取到的两枝铅笔均为正品,所以所求事件的概率为1- 参考答案:C 11.用冒泡法对一组数:37,21,3,56,9,81,7进行排序时,经过若干趟排序后,得到一组数:3,9,21,7,37,56,81,问需要几趟排序才能得到( ) A.2趟 B.3趟 C.4趟 D.5趟 参考答案:B 二、填空题 12.掷两颗骰子,出现点数之和等于8的概率等于__________. 参考答案: 13.某城市有学校500所,其中大学10所,中学200所,小学290所.现在取50所学校作为一个样本进行一项调查,用分层抽样进行抽样,应该选取大学__________所,中学__________所,小学__________所. 参考答案:1 20 29 14.某中学期中考试后,对成绩进行分析,从某班中选出5名学生的总成绩和外语成绩如下表:
则外语成绩对总成绩的回归直线方程是_______________________. 参考答案: 15.用辗转相除法求两个数102、238的最大公约数是__________. 参考答案:34 三、解答题 16.在数学考试中,小丽的成绩在90分以上的概率是0.18,在80~89分的概率是0.51,在70~79分的概率是0.15,在60~69分的概率是0.09.计算小丽在数学考试中取得80分以上成绩的概率和小丽考试及格的概率. 解析:分别记小丽的考试成绩在90分以上、在80~89分、在70~79分、在60~69分分别为事件B、C、D、E,这4个事件是彼此互斥的,根据互斥事件的概率加法公式,小丽的考试成绩在80分以上的概率是 P(B∪C)=P(B)+P(C)=0.18+0.51=0.69. 小丽考试及格的概率,即成绩在60分以上的概率,由公式得 P(B∪C∪D∪E)=P(B)+P(C)+P(D)+P(E)=0.18+0.51+0.15+0.09=0.93. 17.某水产试验厂实行某种鱼的人工孵化,10000个卵能孵化出7645尾鱼苗.根据概率的统计定义解答下列问题: (1)求这种鱼卵的孵化概率(孵化率); (2)30000个鱼卵大约能孵化多少尾鱼苗? (3)要孵化5000尾鱼苗,大概得准备多少鱼卵?(精确到百位) 参考答案:(1)0.7645 (2)22935尾 (3)6500个鱼卵 18.对某400件元件进行寿命追踪调查情况频率分布如下:
(1)列出寿命与频数对应表; (2)估计元件寿命在500~800 h以内的频率; (3)估计元件寿命在800 h以上的频率. 参考答案:(1)寿命与频数对应表:
(2)估计该元件寿命在(500~800)h以内的概率为0.10+0.15+0.40=0.65. (3)估计该元件寿命在700 h以上的概率为0.40+0.20+0.15=0.75. 19.如果你是老师,试设计一个在数学探究课上的教学方案,要求画出流程图.(开放型题,可以有不同的参考答案) 参考答案: 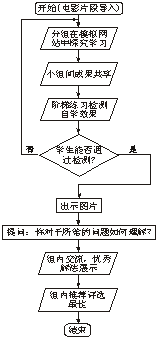 20.用循环语句描述1+ 解:算法分析: 第一步是选择一个变量S表示和,并赋给初值0,再选取一个循环变量i,并赋值为0; 第二步开始进入WHILE循环语句,首先判断i是否小于9; 第三步为循环表达式(循环体),用WEND来控制循环; 第四步用END来结束程序. 可写出程序如下: S=0 i=0 WHILE i<=9 S=S+1/2^i i=i+1 WEND PRINT S END 运行该程序,输出: S=1.9980 21.目前高中毕业会考中,成绩在85~100为“A”,70~84为“B”,60~69为“C”,60分以下为“D”.编制程序,输入学生的考试成绩(百分制,若有小数则四舍五入),输出相应的等级. 参考答案: I=1 WHILE I=1 INPUT “shu ru xue sheng cheng ji a=”;a IF a<60 THEN PRINT “D” ELSE IF a<70 THEN PRINT “C” ELSE IF a<85 THEN PRINT “B” ELSE PRINT “A” END IF END IF END IF INPUT “INPUT 1,INPUT 2”;I WEND END (责任编辑:admin) |
