|
28.(全国Ⅱ•理•19题)如图,在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,E、F分别是AB、SC的中点。 (Ⅰ)求证:EF∥平面SAD;(Ⅱ)设SD = 2CD,求二面角A-EF-D的大小; 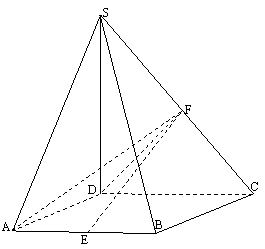 【解答】解法一: (1)作 连结 故 所以 (2)不妨设 取 又 所以 取 连结 故 所以二面角 解法二:(1)如图,建立空间直角坐标系 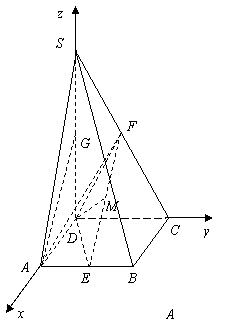 设 取 所以 (2)不妨设 又 所以向量  . .所以二面角 29.(北京•理•16题)如图,在 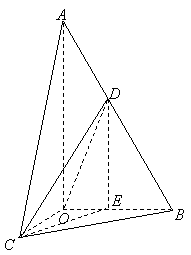 (I)求证:平面 (II)当 (III)求 【解答】解法一: (I)由题意, 又 又 (II)作 在 又 (III)由(I)知, 当 这时, 解法二: (I)同解法一. (II)建立空间直角坐标系 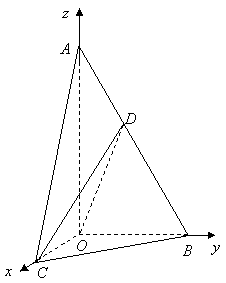  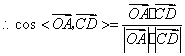 (III)同解法一 30.(安徽•理•17题)如图,在六面体ABCD-A1B1C1D1中,四边形ABCD是边长为2的正方形,四边形A1B1C1D1是边长为1的正方形,DD1⊥平面A1B1C1D1,DD1⊥平面ABCD,DD1=2。 (Ⅰ)求证:A1C1与AC共面,B1D1与BD共面; (Ⅱ)求证:平面A1ACC1⊥平面B1BDD1; (Ⅲ)求二面角A-BB1-C的大小(用反三角函数值圾示); 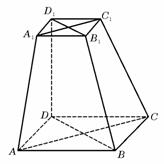 【解答】本小题主要考查直线与平面的位置关系、平面与平面的位置关系、二面角及其平面角等有关知识,考查空间想象能力和思维能力,应用向量知识解决立体几何问题的能力.本小题满分14分. 解法1(向量法): 以   则有 (Ⅰ)证明: 于是 (Ⅱ)证明: 又平面 (Ⅲ)解: 设 于是 设 于是 解法2(综合法): (Ⅰ)证明: 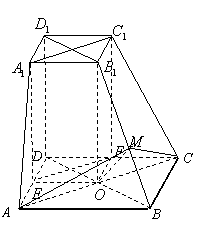  于是 设 有 于是 由 故 过点 则 于是 所以点 (Ⅱ)证明: 又 又平面 (Ⅲ)解: 根据三垂线定理,有 过点 则 于是 所以, 根据勾股定理,有 二面角 (责任编辑:admin) |
