14、(四川理)(本小题满分12分)设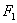 、 、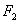 分别是椭圆 分别是椭圆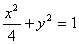 的左、右焦点. 的左、右焦点.
(Ⅰ)若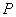 是该椭圆上的一个动点,求 是该椭圆上的一个动点,求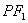 · ·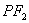 的最大值和最小值; 的最大值和最小值;
(Ⅱ)设过定点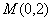 的直线 的直线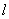 与椭圆交于不同的两点 与椭圆交于不同的两点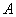 、 、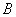 ,且∠ ,且∠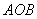 为锐角(其中 为锐角(其中 为坐标原点),求直线 为坐标原点),求直线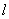 的斜率 的斜率 的取值范围. 的取值范围.
本题主要考察直线、椭圆、平面向量的数量积等基础知识,以及综合应用数学知识解决问题及推理计算能力。
解:(Ⅰ)解法一:易知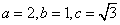
所以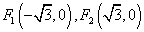 ,设 ,设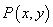 ,则 ,则
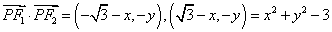 
因为 ,故当 ,故当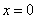 ,即点 ,即点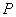 为椭圆短轴端点时, 为椭圆短轴端点时,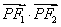 有最小值 有最小值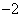
当 ,即点 ,即点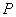 为椭圆长轴端点时, 为椭圆长轴端点时,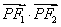 有最大值 有最大值
解法二:易知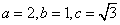 ,所以 ,所以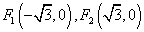 ,设 ,设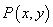 ,则 ,则
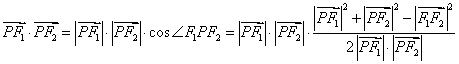
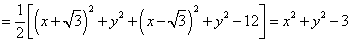 (以下同解法一) (以下同解法一)
(Ⅱ)显然直线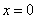 不满足题设条件,可设直线 不满足题设条件,可设直线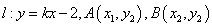 , ,
联立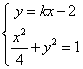 ,消去 ,消去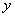 ,整理得: ,整理得: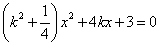
∴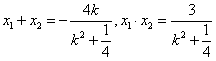
由 得: 得: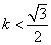 或 或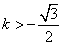
又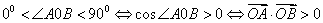
∴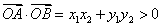
又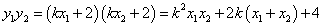  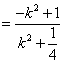
∵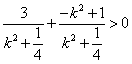 ,即 ,即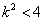 ∴ ∴
故由①、②得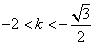 或 或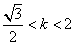
15、(上海理)已知双曲线 ,则以双曲线中心为焦点,以双曲线左焦点为顶点的抛物线方程为 ,则以双曲线中心为焦点,以双曲线左焦点为顶点的抛物线方程为 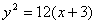
【解析】双曲线 的中心为O(0,0),该双曲线的左焦点为F(-3,0)则抛物线的顶点为(-3,0),焦点为(0,0),所以p=6,所以抛物线方程是) 的中心为O(0,0),该双曲线的左焦点为F(-3,0)则抛物线的顶点为(-3,0),焦点为(0,0),所以p=6,所以抛物线方程是)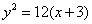
16、(上海理)已知半椭圆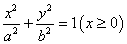 与半椭圆 与半椭圆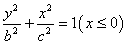 组成的曲线称为“果圆”,其中 组成的曲线称为“果圆”,其中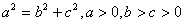 , ,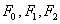 是对应的焦点。 是对应的焦点。
(1)若三角形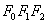 是边长为1的等边三角形,求“果圆”的方程; 是边长为1的等边三角形,求“果圆”的方程;
(2)若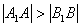 ,求 ,求 的取值范围; 的取值范围;
(3)一条直线与果圆交于两点,两点的连线段称为果圆的弦。是否存在实数 ,使得斜率为 ,使得斜率为 的直线交果圆于两点,得到的弦的中点的轨迹方程落在某个椭圆上?若存在,求出所有 的直线交果圆于两点,得到的弦的中点的轨迹方程落在某个椭圆上?若存在,求出所有 的值;若不存在,说明理由。 的值;若不存在,说明理由。
解(1)∵F0(c,0)F1(0,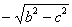 ),F2(0, ),F2(0, ) )
∴| F0F1 |=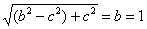 ,| F1F2 |= ,| F1F2 |=
于是 , ,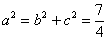 ,所求“果圆”方程为 ,所求“果圆”方程为
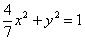 (x≥0), (x≥0), (x≤0). ……4分 (x≤0). ……4分
(2)由题意,得a+c>2b,即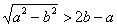 . .
∵(2b)2>b2+c2,∴a2-b2>(2b-a)2,得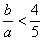 ……7分 ……7分
又b2>c2=a2-b2,∴ . .
∴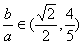 . .
(3)设“果圆”的方程为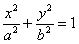 (x≥0) (x≥0) (x≤0) (x≤0)
记平行弦的斜率为k.
当k=0时,直线y=t(-b≤t≤b)与半椭圆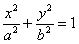 (x≥0)的交点是 (x≥0)的交点是
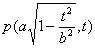 ,与半椭圆 ,与半椭圆 (x≤0)的交点是Q( (x≤0)的交点是Q( ). ).
∴P、Q的中点M(x,y)满足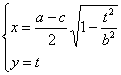
得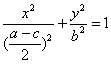 . .
∵a<2b,∴ . .
综上所述,当k=0时,“果圆”平行弦的中点轨迹总是落在某个椭圆……14分
当k>0时,以k为斜率过B1的直线l与半椭圆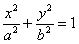 (x≥0)的交点是 (x≥0)的交点是
由此,在直线l右测,以k为斜率的平行弦的中点轨迹在直线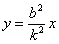 上,即不在某一椭圆上. ……17分 上,即不在某一椭圆上. ……17分
当k<0时,可类似讨论得到平行弦中点轨迹不都在某一椭圆上. ……18分
17、(上海文)我们把由半椭圆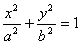 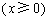 与半椭圆 与半椭圆 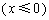 合成的曲线称作“果圆”,其中 合成的曲线称作“果圆”,其中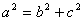 , , , , .如图,设点 .如图,设点 , ,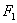 , ,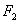 是相应椭圆的焦点, 是相应椭圆的焦点,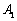 , ,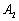 和 和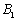 , ,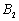 是“果圆” 与 是“果圆” 与 , ,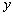 轴的交点, 轴的交点,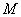 是线段 是线段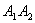 的中点. 的中点.
 
(1)若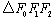 是边长为1的等边三角形,求该 是边长为1的等边三角形,求该
“果圆”的方程;
(2)设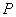 是“果圆”的半椭圆 是“果圆”的半椭圆
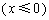 上任意一点.求证:当 上任意一点.求证:当 取得最小值时, 取得最小值时,
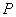 在点 在点 或 或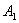 处; 处;
(3)若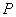 是“果圆”上任意一点,求 是“果圆”上任意一点,求 取得最小值时点 取得最小值时点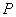 的横坐标. 的横坐标.
解:(1)  , ,
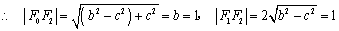 , ,
于是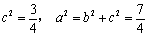 , ,
所求“果圆”方程为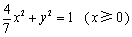 , ,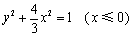 . .
(2)设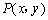 ,则 ,则

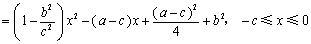 , ,
 , ,  的最小值只能在 的最小值只能在 或 或 处取到. 处取到.
即当 取得最小值时, 取得最小值时,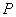 在点 在点 或 或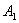 处. 处.
(3)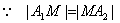 ,且 ,且 和 和 同时位于“果圆”的半椭圆 同时位于“果圆”的半椭圆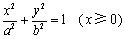 和半椭圆 和半椭圆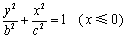 上,所以,由(2)知,只需研究 上,所以,由(2)知,只需研究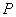 位于“果圆”的半椭圆 位于“果圆”的半椭圆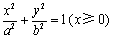 上的情形即可. 上的情形即可.

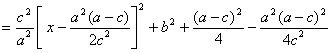 . .
当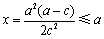 ,即 ,即 时, 时, 的最小值在 的最小值在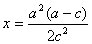 时取到, 时取到,
此时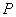 的横坐标是 的横坐标是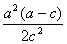 . .
当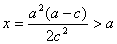 ,即 ,即 时,由于 时,由于 在 在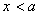 时是递减的, 时是递减的, 的最小值在 的最小值在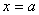 时取到,此时 时取到,此时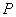 的横坐标是 的横坐标是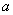 . .
综上所述,若 ,当 ,当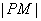 取得最小值时,点 取得最小值时,点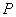 的横坐标是 的横坐标是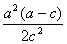 ;若 ;若 ,当 ,当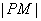 取得最小值时,点 取得最小值时,点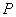 的横坐标是 的横坐标是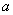 或 或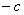 . .
18、(陕西文)抛物线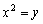 的准线方程是 的准线方程是
(A)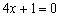 (B) (B)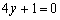
(C)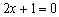 (D) (D)
解析:P=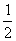 ,准线方程为y= ,准线方程为y= ,即 ,即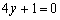 ,选B ,选B
19、(陕西文)已知双曲线C∶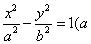 >0,b>0),以C的右焦点为圆心且与C的渐近线相切的圆的半径是 >0,b>0),以C的右焦点为圆心且与C的渐近线相切的圆的半径是
(A)a (B)b (C)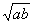 (D) (D)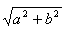
解析:圆的半径是(C,0)到渐近线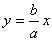 的距离,所以R= 的距离,所以R= ,选B ,选B
20、(陕西文)(本小题满分14分)已知椭圆C: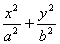 =1(a>b>0)的离心率为 =1(a>b>0)的离心率为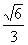 ,短轴一个端点到右焦点的距离为 ,短轴一个端点到右焦点的距离为 . .
(Ⅰ)求椭圆C的方程;
(Ⅱ)设直线l与椭圆C交于A、B两点,坐标原点O到直线l的距离为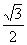 ,求△AOB面积的最大值. ,求△AOB面积的最大值.
解:(Ⅰ)设椭圆的半焦距为 ,依题意 ,依题意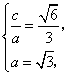
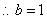 , , 所求椭圆方程为 所求椭圆方程为 . .
(Ⅱ)设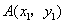 , ,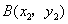 . .
(1)当 轴时, 轴时,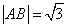 . .
(2)当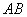 与 与 轴不垂直时, 轴不垂直时,
设直线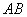 的方程为 的方程为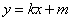 . .
由已知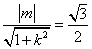 ,得 ,得 . .
把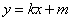 代入椭圆方程,整理得 代入椭圆方程,整理得 , ,
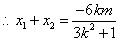 , ,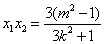 . .
 

 . .
当且仅当 ,即 ,即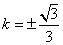 时等号成立.当 时等号成立.当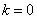 时, 时,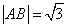 , ,
综上所述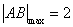 . .
 当 当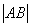 最大时, 最大时, 面积取最大值 面积取最大值 . .
21、(山东理)设 是坐标原点, 是坐标原点,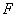 是抛物线 是抛物线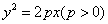 的焦点, 的焦点,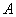 是抛物线上的一点, 是抛物线上的一点,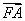 与 与 轴正向的夹角为 轴正向的夹角为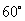 ,则 ,则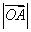 为 . 为 .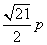
【分析】:过A 作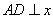 轴于D,令 轴于D,令 ,则 ,则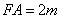 , , , ,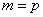 。 。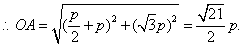
(责任编辑:admin) |
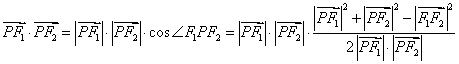
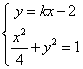 ,消去
,消去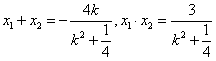

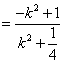
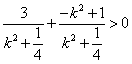 ,即
,即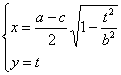
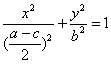 .
.

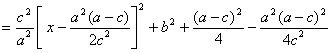 .
.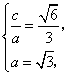

 .
.