|
22、(山东理)(本小题满分12分)已知椭圆 (Ⅰ)求椭圆 (Ⅱ)若直线 【解答】(I)由题意设椭圆的标准方程为 (II)设 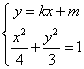 得 得当 当 综上可知,直线 23、(全国2理)设 A. 【解答】设F1,F2分别是双曲线 24、(全国2理)设 A.9 B.6 C.4 D.3 【解答】设F为抛物线y2=4x的焦点,A、B、C为该抛物线上三点,若 ∴ |FA|+|FB|+|FC|= 25、(全国2理)(本小题满分12分)在直角坐标系 (1)求圆 (2)圆 【解答】(1)依题设,圆 即 得圆 (2)不妨设 设 即  由于点 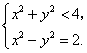 由此得 所以 26、(全国2文)已知椭圆的长轴长是短轴长的2倍,则椭圆的离心率等于( ) A. 【解答】已知椭圆的长轴长是短轴长的2倍,∴ 27、(全国2文)设 A. 【解答】设 28、(全国1理)已知双曲线的离心率为 A. 【解答】已知双曲线的离心率为2,焦点是 29、(全国1理)抛物线 A. 【解答】抛物线 30、(全国1理)(本小题满分12分)已知椭圆 (Ⅰ)设 (Ⅱ)求四边形 【解答】(Ⅰ)证明:椭圆的半焦距 由 所以, (Ⅱ)(ⅰ)当 设 因为 所以,  . .四边形  . .当 (ⅱ)当 综上,四边形 31、(海南、宁夏理)已知抛物线 A. C. 【分析】:由抛物线定义, 32、(海南、宁夏理)已知双曲线的顶点到渐近线的距离为2,焦点到渐近线的距离为6,则该双曲线的离心率为 .3 【分析】:如图,过双曲线的顶点A、焦点F分别向其渐近线作垂线,垂足分别为B、C,则:  33、(海南、宁夏理)(本小题满分12分)在平面直角坐标系 (I)求 (II)设椭圆与 【解答】(Ⅰ)由已知条件,直线 代入椭圆方程得 整理得 直线 解得 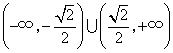 . .(Ⅱ)设 由方程①, 又 而 所以 将②③代入上式,解得 由(Ⅰ)知 34、(辽宁理)设 A. 【解答】因为 35、(辽宁理)设椭圆 【解答】椭圆 36、(辽宁理)(本小题满分14分)已知正三角形 (I)求圆 (II)设圆 【解答】本小题主要考查平面向量,圆与抛物线的方程及几何性质等基本知识,考查综合运用解析几何知识解决问题的能力.满分14分. (I)解法一:设  , , ,由题设知 ,由题设知 . .解得 所以 设圆心 解法二:设 又因为 由 设  ,于是有 ,于是有 ,解得 ,解得(II)解:设 在 所以 则 (责任编辑:admin) |
