|
31.(福建•理•18题)如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点。 (Ⅰ)求证:AB1⊥面A1BD; (Ⅱ)求二面角A-A1D-B的大小; (Ⅲ)求点C到平面A1BD的距离; 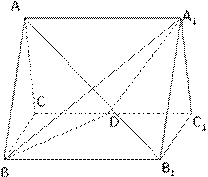 【解答】本小题主要考查直线与平面的位置关系,二面角的大小,点到平面的距离等知识,考查空间想象能力、逻辑思维能力和运算能力.满分12分. 解法一:(Ⅰ)取  连结 在正方形 (Ⅱ)设 在 又 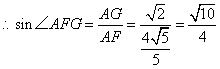 . .所以二面角 (Ⅲ) 在正三棱柱中, 设点 由 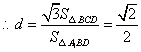 . .解法二:(Ⅰ)取 取 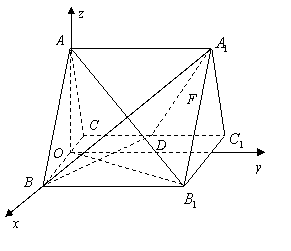 (Ⅱ)设平面   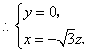 令 由(Ⅰ)知 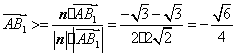 . .(Ⅲ)由(Ⅱ),  . .32.(广东•理•19题)如图6所示,等腰△ABC的底边AB=6 (Ⅰ)求V(x)的表达式; (Ⅱ)当x为何值时,V(x)取得最大值? (Ⅲ)当V(x)取得最大值时,求异面直线AC与PF所成角的余弦值;  【解答】(1)由折起的过程可知,PE⊥平面ABC, V(x)= (2) (3)过F作MF//AC交AD与M,则 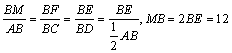 ,PM= ,PM=在△PFM中, 33.(湖北•理•18题)如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=θ (Ⅰ)求证:平面VAB⊥平面VCD ; (Ⅱ)当角θ变化时,求直线BC与平面VAB所成的角的取值范围; 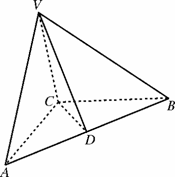 【解答】本小题主要考查线面关系、直线与平面所成角的有关知识,考查空间想象能力和推理运算能力以及应用向量知识解决数学问题的能力. 解法1:(Ⅰ) 又 (Ⅱ) 过点 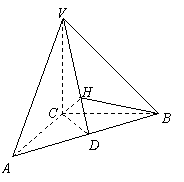  在 设 又 即直线 解法2:(Ⅰ)以 则 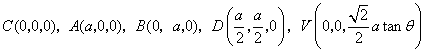 , ,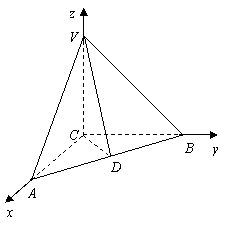  于是, 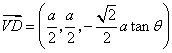 , ,从而 同理 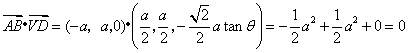 , ,即 又 (Ⅱ)设直线 则由 得 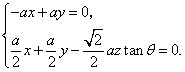 可取 于是 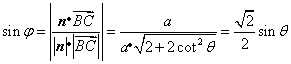 , ,又 即直线 解法3:(Ⅰ)以点 则  , , , ,于是 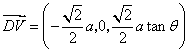 , ,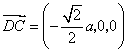 , ,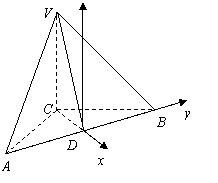  从而 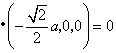 ,即 ,即同理  ,即 ,即又 又 (Ⅱ)设直线 则由 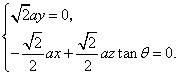 可取 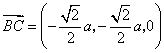 , ,于是  , ,又 即直线 解法4:以 则 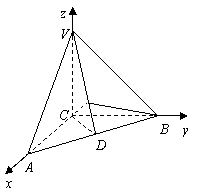  (Ⅰ) 即 即 又 又 (Ⅱ)设直线 设 则 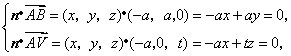 取 取可取 于是  , ,即直线 (责任编辑:admin) |
