|
41、（广东理）如图6所示，等腰三角形△ABC的底边AB=  ，高CD=3，点E是线段BD上异于B、D的动点，点F在BC边上，且EF⊥AB，现沿EF将△BEF折起到△PEF的位置，使PE⊥AE，记BE=x，V（x）表示四棱锥P-ACEF的体积。（1）求V(x)的表达式； （2）当x为何值时，V(x)取得最大值？ （3）当V（x）取得最大值时，求异面直线AC与PF所成角的余弦值。  （1）由折起的过程可知，PE⊥平面ABC，  ， V(x)=  （ ）（2）  ，所以 时， ，V(x)单调递增； 时 ，V(x)单调递减；因此x=6时，V(x)取得最大值 ；（3）过F作MF//AC交AD与M,则 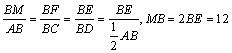 ，PM= ， ，在△PFM中，  ，∴异面直线AC与PF所成角的余弦值为 ；42、（广东理）已知函数  ， 是方程f(x)=0的两个根 ， 是f(x)的导数；设 ， （n=1,2,……）（1）求 的值；（2）证明：对任意的正整数n，都有  >a；（3）记  （n=1,2,……），求数列{bn}的前n项和Sn。解析：（1）∵ ，是方程f(x)=0的两个根，∴  ；（2）  ， =  ，∵，∴有基本不等式可知 （当且仅当 时取等号），∴ 同，样 ，……， （n=1,2,……），（3）  ，而 ，即 ， ，同理 ， ，又  43、（福建理）已知函数  （Ⅰ）若  ，试确定函数 的单调区间；（Ⅱ）若  ，且对于任意 ， 恒成立，试确定实数 的取值范围；（Ⅲ）设函数  ，求证： ．本小题主要考查函数的单调性、极值、导数、不等式等基本知识，考查运用导数研究函数性质的方法，考查分类讨论、化归以及数形结合等数学思想方法，考查分析问题、解决问题的能力．满分14分． 解：（Ⅰ）由 得 ，所以 ．由  得 ，故的单调递增区间是 ，由  得 ，故的单调递减区间是 ．（Ⅱ）由  可知 是偶函数．于是 对任意成立等价于 对任意 成立．由  得 ．①当  时， ．此时 在 上单调递增．故  ，符合题意．②当  时， ．当  变化时 的变化情况如下表：
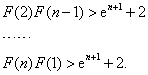由此可得，在 上， ．依题意，  ，又 ．综合①，②得，实数 的取值范围是 ．（Ⅲ）  ，  ， ， 由此得，  故  ．44、（北京理）如图，有一块半椭圆形钢板，其半轴长为 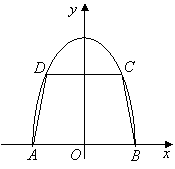 ，短半轴长为 ，计划将此钢板切割成等腰梯形的形状，下底 是半椭圆的短轴，上底 的端点在椭圆上，记 ，梯形面积为 ．（I）求面积 以为自变量的函数式，并写出其定义域；（II）求面积 的最大值． 解：（I）依题意，以 的中点 为原点建立直角坐标系 （如图），则点 的横坐标为． 点 的纵坐标 满足方程 ，解得    ，其定义域为  ．（II）记  ，则  ．令 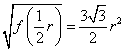 ，得 ．因为当  时，；当 时，，所以 是的最大值．因此，当 时，也取得最大值，最大值为 ．即梯形面积 的最大值为 ．45、（安徽理）设a≥0，f(x)=x－1－ln2 x＋2aln x（x>0）. （Ⅰ）令F（x）＝xf＇（x），讨论F（x）在（0.＋∞）内的单调性并求极值； （Ⅱ）求证：当x>1时，恒有x>ln2x－2aln x＋1. 本小题主要考查函数导数的概念与计算，利用导数研究函数的单调性、极值和证明不等式的方法，考查综合运用有关知识解决问题的能力．本小题满分14分． （Ⅰ）解：根据求导法则有  ，故  ，于是  ，列表如下：
故知  在 内是减函数，在 内是增函数，所以，在 处取得极小值 ．（Ⅱ）证明：由  知，的极小值 ．于是由上表知，对一切  ，恒有 ．从而当  时，恒有，故在 内单调增加．所以当 时， ，即 ．故当 时，恒有 ．(责任编辑：admin) |
