【考题回放】
1文.函数 是减函数的区间为(D) 是减函数的区间为(D)
A.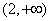 B. B.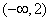 C. C. D. D.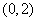
1(理)函数y=xcosx-sinx在下面哪个区间内是增函数(B )
A (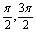 ) B (π,2π) C ( ) B (π,2π) C ( ) D (2π,3π) ) D (2π,3π)
2.若曲线 的一条切线 的一条切线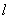 与直线 与直线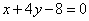 垂直,则 垂直,则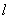 的方程为A 的方程为A
A. B. B.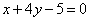
C.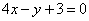 D. D.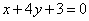
3.函数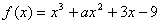 ,已知 ,已知 在 在 时取得极值,则 时取得极值,则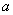 =(B) =(B)
A.2 B.3 C.4 D.5
4.在函数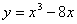 的图象上,其切线的倾斜角小于 的图象上,其切线的倾斜角小于 的点中,坐标为整数的点的个数是 ( D ) 的点中,坐标为整数的点的个数是 ( D )
A.3 B.2 C.1 D.0
5.曲线y=x3在点(1,1)处的切线与x轴、直线x=2所围成的三角形的面积为______8/3____
6.设a为实数,函数
(Ⅰ)求 的极值. 的极值.
(Ⅱ)当a在什么范围内取值时,曲线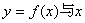 轴仅有一个交点. 轴仅有一个交点.
【解答】:(I)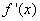 =3 =3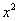 -2 -2 -1 -1
若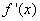 =0,则 =0,则 =- =-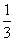 , , =1 =1
当 变化时, 变化时,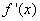 , , 变化情况如下表: 变化情况如下表:

|
(-∞,-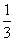 ) )
|
-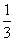
|
(-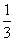 ,1) ,1)
|
1
|
(1,+∞)
|
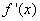
|
+
|
0
|
-
|
0
|
+
|

|

|
极大值
|

|
极小值
|

|
∴ 的极大值是 的极大值是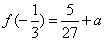 ,极小值是 ,极小值是
(II)函数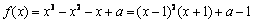
由此可知,取足够大的正数时,有 >0,取足够小的负数时有 >0,取足够小的负数时有 <0,所以曲线 <0,所以曲线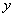 = = 与 与 轴至少有一个交点 轴至少有一个交点
结合 的单调性可知: 的单调性可知:
当 的极大值 的极大值 <0,即 <0,即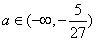 时,它的极小值也小于0,因此曲线 时,它的极小值也小于0,因此曲线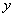 = = 与 与 轴仅有一个交点,它在(1,+∞)上。 轴仅有一个交点,它在(1,+∞)上。
当 的极小值 的极小值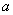 -1>0即 -1>0即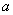  (1,+∞)时,它的极大值也大于0,因此曲线 (1,+∞)时,它的极大值也大于0,因此曲线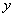 = = 与 与 轴仅有一个交点,它在(-∞,- 轴仅有一个交点,它在(-∞,-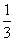 )上。 )上。
∴当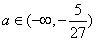 ∪(1,+∞)时,曲线 ∪(1,+∞)时,曲线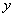 = = 与 与 轴仅有一个交点 轴仅有一个交点
(责任编辑:admin) |
