|
39、(陕西理)已知各项全不为零的数列{ak}的前k项和为Sk,且Sk= (Ⅰ)求数列{ak}的通项公式; (Ⅱ)对任意给定的正整数n(n≥2),数列{bk}满足 解:(Ⅰ)当 当 因为 (Ⅱ)因为 所以 故 40、(陕西文)已知实数列 (Ⅰ)求数列 (Ⅱ)数列 解:(Ⅰ)设等比数列 由 因为 即 所以 (Ⅱ) 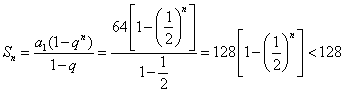 . .41、(山东理)设数列 (Ⅰ)求数列 (Ⅱ)设 解:(I) 验证 (II) 42、(山东文)设 (1)求数列 (2)令 解:(1)由已知得  解得 设数列 又 即 解得 由题意得 故数列 (2)由于 由(1)得 又 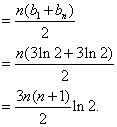 故 43、(全国2理)设数列 (1)求 (2)设 解:(1)由 整理得 又 (2)方法一: 由(1)可知 那么, 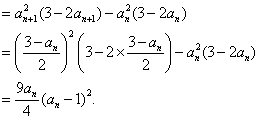 又由(1)知 因此 方法二: 由(1)可知 因为 所以 由 即 两边开平方得 即 44、(全国2文)设等比数列 解:由题设知 则  ② ②由②得 因为 当 当 45、(全国1理)已知数列 (Ⅰ)求 (Ⅱ)若数列 证明: 解:(Ⅰ)由题设: 所以,数列 即 (Ⅱ)用数学归纳法证明. (ⅰ)当 (ⅱ)假设当 也即 当 又 所以 也就是说,当 根据(ⅰ)和(ⅱ)知 46、(全国1文)设 (Ⅰ)求 (Ⅱ)求数列 解:(Ⅰ)设 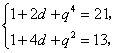 解得 所以 (Ⅱ) ②-①得 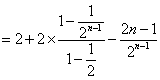 (责任编辑:admin) |
