|
【考题回放】 1．设数列｛an｝的首项a1＝－7，且满足an＋1＝an＋2（n∈N），则a1＋a2＋……＋a17＝ 153 . 2．已知数列  、 都是公差为1的等差数列，其首项分别为 、 ，且  ， ．设 （ ），则数列 的前10项和等于（ C ）（A）55 （B）70 （C）85 （D）100 3．在等比数列  中， ，前 项和为 ，若数列 也是等比数列，则等于（ C ）(A)  (B)  (C)  (D) 4. 若干个能唯一确定一个数列的量称为该数列的“基本量”．设{an}是公比为q的无穷等比数列，下列{an}的四组量中：①S1与S2； ②a2与S3； ③a1与an； ④q与an．其中一定能成为该数列“基本量”的是第 ①④ 组．(写出所有符合要求的组号) 5．设数列{an}的首项 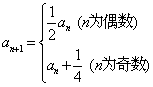 ，且 ，记 ．（I）求a2，a3； （II）判断数列{bn}是否为等比数列，并证明你的结论； （III）（理）求  ．【解答】 （I）a2＝a1+  = a+，a3= a2 =a+ ；（II）∵a4 = a3+ =a+ ， ∴a5=a4=a+ ，所以b1=a1－ =a－， b2=a3－= (a－)， b3=a5－= (a－)，猜想：{bn}是公比为 的等比数列．证明如下：因为bn+1＝a2n+1－ =a2n－= (a2n－1－)=bn，(n∈N*)所以{bn}是首项为a－ ， 公比为的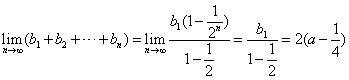等比数列·（III）（理）  ． (责任编辑：admin) |