|
1（全国2理科）.不等式:  >0的解集为（C）(A)( -2, 1) (B) ( 2, +∞) (C) ( -2, 1)∪ ( 2, +∞) (D) ( -∞, -2)∪ ( 1, +∞) 2．（北京理科6）若不等式组 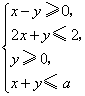 表示的平面区域是一个三角形，则 的取值范围是（ D ）A．  B． C． D．或3．（北京理科7）如果正数  满足 ，那么（ A ）A．  ，且等号成立时的取值唯一B．  ，且等号成立时的取值唯一C． ，且等号成立时的取值不唯一D． ，且等号成立时的取值不唯一4．（北京理科12）已知集合  ， ．若 ，则实数的取值范围是 （2，3） ．5（上海理科6）已知  ，且 ，则 的最大值为  6．(上海理科13)已知  为非零实数，且 ，则下列命题成立的是(C)A、  B、 C、 D、 7．(上海理科15)已知  是定义域为正整数集的函数，对于定义域内任意的 ，若 成立，则 成立，下列命题成立的是（D）A、若  成立，则对于任意 ，均有成立B、若  成立，则对于任意的 ，均有 成立C、若  成立，则对于任意的 ，均有成立D、若  成立，则对于任意的，均有成立8（天津理科2）设变量 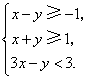 满足约束条件 则目标函数 的最大值为（ B ）A．4 B．11 C．12 D．14 9（天津理科9）设 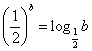 均为正数，且 ， ， ．则（ A ）A．  B． C． D． 10．（浙江理科1）“  ”是“ ”的（A）（A）充分而不必要条件 （B）必要而不充分条件 （C）充分必要条件 （D）既不充分也不必要条件 【分析】：由 可得 , 可得到,但得不到.故选A.11．（浙江理科13）不等式  的解集是_____________。 【分析】：   12．（浙江理科17）设  为实数，若 ，则的取值范围是_____________。 【分析】：作图易知,设  若 不成立;故当  且斜率大于等于 时方成立.13．（湖北理科3）3.设P和Q是两个集合，定义集合P-Q=  ，如果P={x|log2x<1},Q={x||x-2|<1},那么P-Q等于（B）A．{x|0<x<1} B.{x|0<x≤1} C.{x|1≤x<2} D.{x|2≤x<3} 14．（湖北理科21）（本小题满分14分）已知m，n为正整数. （Ⅰ）用数学归纳法证明：当x>-1时，  ≥1+mx；（Ⅱ）对于n≥6，已知  ，求证 ，m=1,1,2…，n；（Ⅲ）求出满足等式  的所有正整数n.解：（Ⅰ）证：当x=0或m=1时，原不等式中等号显然成立，下用数学归纳法证明： 当x>-1，且x≠0时，m≥2,(1+x)m>1+mx. 1 (i)当m=2时，左边＝1+2x+  ,右边＝1+2x，因为x≠0,所以>0，即左边>右边，不等式①成立；（ii）假设当m=k(k≥2)时，不等式①成立，即  >1+kx,则当m=k+1时，因为x>-1,所以1+x>0.又因为x≠0,k≥2,所以k>0.于是在不等式 >1+kx两边同乘以1+x得（1+x）k·(1+x)>(1+kx)(1+x)=1+(k+1)x+k >1+(k+1)x,所以  >1+(k+1)x,即当m＝k+1时，不等式①也成立.综上所述，所证不等式成立. (Ⅱ)证：当  而由（Ⅰ），   （Ⅲ）解：假设存在正整数  成立，即有（  ）+ ＝1. ②又由（Ⅱ）可得 （ ）+ +  与②式矛盾，故当n≥6时，不存在满足该等式的正整数n. 故只需要讨论n=1,2,3,4,5的情形； 当n=1时，3≠4，等式不成立； 当n=2时，  ，等式成立；当n=3时，  ，等式成立；当n=4时，  为偶数，而 为奇数，故 ,等式不成立；当n=5时，同n=4的情形可分析出，等式不成立. 综上，所求的n只有n=2,3. 15（湖南理科2）．不等式  的解集是（ D ）A．  B． C． D． 16（湖南理科14）．设集合  ， ，，（1）  的取值范围是 ；（2）若  ，且 的最大值为9，则的值是 ．（1）  （2） 17．（福建理科3）已知集合A＝  ，B＝ ，且 ，则实数的取值范围是（C）A．  B． a<1 C． D．a>218．（福建理科7）已知  为R上的减函数，则满足 的实数 的取值范围是（C）A．（－1，1） B．（0，1） C．（－1，0）  （0，1） D．（－ ，－1）（1，＋）19．（福建理科13）已知实数x、y满足 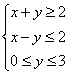 ，则 的取值范围是___ _______；20．（重庆理科2）命题“若  ，则 ”的逆否命题是（D）A．若  ，则 或 B.若，则C.若  或 ，则 D.若或，则21．（重庆理科13）若函数f(x) =  的定义域为R，则a的取值范围为_______. 【分析】：  恒成立， 恒成立，22．(江西理科17)．（本小题满分12分）已知函数  在区间(0，1)内连续，且 ．（1）求实数k和c的值； （2）解不等式  解：（1）因为  ，所以 ，由  ，即 ， ．又因为  在 处连续，所以  ，即 ．（2）由（1）得：  由  得，当 时，解得 ．当  时，解得 ，所以 的解集为 ．23．（山东理科2）．已知集合  ， 则 （B）(A)  (B)  (C)  (D)  24．(山东理科16)函数y=loga(x+3)-1(a>0,a  1)的图象恒过定点A，若点A在直线mx+ny+1=0上，其中mn>0,则 的最小值为 . 8【分析】：函数  的图象恒过定点 ， ， ， ， 25．(安徽理科3)若对任意  R,不等式 ≥ax恒成立，则实数a的取值范围是（B）(A)a＜-1 (B)  ≤1 (C) ＜1 （D）a≥1 26．（安徽理科5）若  ， ，则 的元素个数为（C）【分析】：  = ， = ，∴ =，其中的元素个数为2，选C。（A）0 （B）1 （C）2 （D）3 27．（江苏6）设函数 定义在实数集上，它的图像关于直线 对称，且当 时， ，则有（B）A．  B． C．  D． 【分析】：利用对称性，三点到直线 距离越远越大28．（陕西理科9）给出如下三个命题：ZXXK.COM ①四个非零实数a、b、c、d依次成等比数列的充要条件是ad=bc;ZXXK.COM ②设a,b∈R，则ab≠0若  ＜1，则 ＞1；ZXXK.COM③若f(x)=log  2x=x,则f（|x|）是偶函数.ZXXK.COM其中不正确命题的序号是 A.①②③ B.①② C.②③ D.①③ZX 【分析】：①ad=bc不一定使a、b、c、d依次成等比数列，如取a=d=-1，b=c=1；②a、b异号时不正确，选B 29（全国1文科1）设  ， ，则 A．  B． C． D． 【分析】：设 ={x| x>－ }，={x| x< }，则，选D。30．（北京文科15）（本小题共12分） 记关于 的不等式 的解集为 ，不等式 的解集为 ．（I）若  ，求；（II）若  ，求正数的取值范围．解：（I）由  ，得 ．（II）  ．由  ，得 ，又，所以 ，即 的取值范围是 ．31．（天津文科1）（1）已知集合  ， ，则（ B ）A．  B． C． D． 32．(浙江文科3)“x＞1”是“x2＞x”的（A） (A)充分而不必要条件 (B)必要而不充分条件 (C)充分必要条件 (D)既不充分也不必要条件 33．湖南文科1．不等式 的解集是（ D ）A．  B． C． D． 34．湖南文科14．设集合 ，，，（1）的取值范围是 ；（2）若，且的最大值为9，则的值是 ．（1）  （2）35．福建文科4．“  ”是“ ”的什么条件……（A ）A．充分而不必要 B．必要而不充分 C．充要 D．既不充分也不必要 36．福建文科7．已知 是R上的减函数，则满足 的实数x的取值范围是（D ）A．  B． C． D． 37．（重庆文科5）“-1＜x＜1”是“x2＜1”的（A） （A）充分必要条件 （B）充分但不必要条件 （C）必要但不充分条件 （D）既不充分也不必要条件 38．（安徽文科16）（本小题满分10分）解不等式  ＞0.解：因为对任意  ， ，所以原不等式等价于 ．即  ， ， ，故解为 ．所以原不等式的解集为  ．39．（广东文科1）．已知集合M={x|1+x>0}，N={x|  >0}，则M∩N=（C）A．{x|-1≤x＜1 B．{x|x>1} C．{x|-1＜x＜1} D．{x|x≥-1} (责任编辑：admin) |