|
湖南省益阳市赫山区第一中学 谢华 直线与圆以及直线与椭圆有关理论无论是它在理论上还是它在应用上都特别重要。因此它的研究受到了广泛的重视。特别是在中学教材、中学有关的杂志、高考试题、高中数学竞赛中涉及这方面的问题也就更多了。下面就给出坐标变换法来将直线与圆以及直线与椭圆位置关系统一起来。 定理：设直线L：   曲线C：  + =1 （a>0,b>0）,直线L与曲线C相离   > ;直线L与曲线C相切 =;直线L与曲线C相交 <.注：对于曲线C： +=1  我们根据圆和椭圆的定义可以知道：当 时曲线C表示圆，当  时曲线C表示椭圆。所以我们只需经研究直线L与曲线C的关系就将直线与圆以及直线与椭圆的关系给统一起来了。 证明：作变换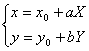：  则经过该变换后曲线方程C和直线方程L分别变成了 曲线C1：  和直线L1： 。由于该线性变换为1-1变换，则在x-o-y直角坐标系下曲线C和直线L的位置关系经过上述变换后在X-O-Y直角坐标系下的曲线C1和直线L1的位置关系不变。反过来，在X-O-Y直角坐标系下的曲线C1和直线L1的位置关系经过上述变换的逆变换后在x-o-y直角坐标系下曲线C和直线L的位置关系不变。所以只需研究经过上述变换后的曲线C1和直线L1的位置关系就可以得出曲线C和直线L的位置。由曲线C1的方程形式知曲线C1是表示圆。根据直线与圆的位置关系知只需判断圆心到直线的距离与圆的半径的大小便可判定圆与直线的位置关系。 ∴ 直线L1与曲线C1相离 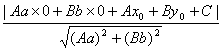 >1 >;直线L1与曲线C1相切 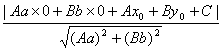=1 =；直线L1与曲线C1相交 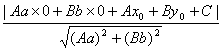<1 <。由于曲线C与直线L相离、相切、相交 曲线C1与直线L1相离、相切、相交。∴ 直线L与曲线C相离 >;直线L与曲线C相切 =;直线L与曲线C相交 <.(责任编辑：admin) |