湖南省常德市安乡县第五中学 龚光勇收集整理
1、导数的背景:(1)切线的斜率;(2)瞬时速度;(3)边际成本。
如一物体的运动方程是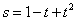 ,其中 ,其中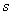 的单位是米, 的单位是米, 的单位是秒,那么物体在 的单位是秒,那么物体在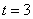 时的瞬时速度为_____(答:5米/秒) 时的瞬时速度为_____(答:5米/秒)
2、导函数的概念:如果函数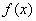 在开区间(a,b)内可导,对于开区间(a,b)内的每一个 在开区间(a,b)内可导,对于开区间(a,b)内的每一个 ,都对应着一个导数 ,都对应着一个导数  ,这样 ,这样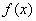 在开区间(a,b)内构成一个新的函数,这一新的函数叫做 在开区间(a,b)内构成一个新的函数,这一新的函数叫做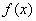 在开区间(a,b)内的导函数,记作 在开区间(a,b)内的导函数,记作 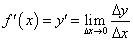
 ,导函数也简称为导数。 ,导函数也简称为导数。
3、求 在 在 处的导数的步骤: 处的导数的步骤:
(1)求函数的改变量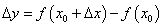 ; ;
(2)求平均变化率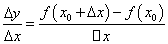 ; ;
(3)取极限,得导数 。 。
4、导数的几何意义:函数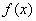 在点 在点 处的导数的几何意义,就是曲线 处的导数的几何意义,就是曲线 在点 在点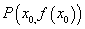 处的切线的斜率,即曲线 处的切线的斜率,即曲线 在点 在点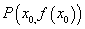 处的切线的斜率是 处的切线的斜率是 ,相应地切线的方程是 ,相应地切线的方程是 。特别提醒:(1)在求曲线的切线方程时,要注意区分所求切线是曲线上某点处的切线,还是过某点的切线:曲线上某点处的切线只有一条,而过某点的切线不一定只有一条,即使此点在曲线上也不一定只有一条;(2)在求过某一点的切线方程时,要首先判断此点是在曲线上,还是不在曲线上,只有当此点在曲线上时,此点处的切线的斜率才是 。特别提醒:(1)在求曲线的切线方程时,要注意区分所求切线是曲线上某点处的切线,还是过某点的切线:曲线上某点处的切线只有一条,而过某点的切线不一定只有一条,即使此点在曲线上也不一定只有一条;(2)在求过某一点的切线方程时,要首先判断此点是在曲线上,还是不在曲线上,只有当此点在曲线上时,此点处的切线的斜率才是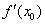 。比如: 。比如:
(1)P在曲线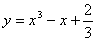 上移动,在点P处的切线的倾斜角为α,则α的取值范围是______(答: 上移动,在点P处的切线的倾斜角为α,则α的取值范围是______(答: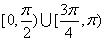 ); );
(2)直线 是曲线 是曲线 的一条切线,则实数 的一条切线,则实数 的值为_______(答:-3或1); 的值为_______(答:-3或1);
(3)已知函数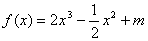 ( (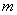 为常数)图象上 为常数)图象上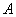 处的切线与 处的切线与 的夹角为 的夹角为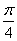 ,则 ,则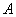 点的横坐标为_____(答:0或 点的横坐标为_____(答:0或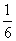 ); );
(4)曲线 在点 在点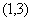 处的切线方程是______________(答: 处的切线方程是______________(答: ); );
(5)已知函数 ,又导函数 ,又导函数 的图象与 的图象与 轴交于 轴交于 。①求 。①求 的值;②求过点 的值;②求过点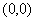 的曲线 的曲线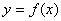 的切线方程(答:①1;② 的切线方程(答:①1;②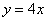 或 或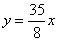 )。 )。
5、导数的运算法则:(1)常数函数的导数为0,即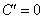 (C为常数); (2) (C为常数); (2) ,与此有关的如下: ,与此有关的如下: ;(3)若 ;(3)若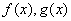 有导数,则① 有导数,则①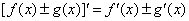 ;② ;②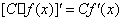 。比如: 。比如:
(1)已知函数 的导数为 的导数为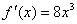 ,则 ,则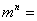 _____(答: _____(答: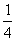 ); );
(2)函数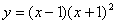 的导数为__________(答: 的导数为__________(答: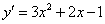 ); );
(3)若对任意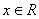 , , ,则 ,则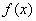 是______(答: 是______(答: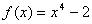 ) )
6、多项式函数的单调性:
(1)多项式函数的导数与函数的单调性:
①若 ,则 ,则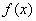 为增函数;若 为增函数;若 ,则 ,则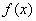 为减函数;若 为减函数;若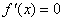 恒成立,则 恒成立,则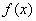 为常数函数;若 为常数函数;若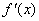 的符号不确定,则 的符号不确定,则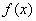 不是单调函数。 不是单调函数。
②若函数 在区间( 在区间( )上单调递增,则 )上单调递增,则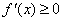 ,反之等号不成立;若函数 ,反之等号不成立;若函数 在区间( 在区间( )上单调递减,则 )上单调递减,则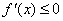 ,反之等号不成立。比如: ,反之等号不成立。比如:
(1)函数 ,其中 ,其中 为实数,当 为实数,当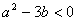 时, 时,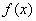 的单调性是______(答:增函数); 的单调性是______(答:增函数);
(2)设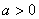 函数 函数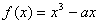 在 在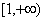 上单调函数,则实数 上单调函数,则实数 的取值范围______(答: 的取值范围______(答: ); );
(3)已知函数 为常数)在区间 为常数)在区间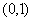 上单调递增,且方程 上单调递增,且方程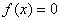 的根都在区间 的根都在区间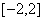 内,则 内,则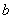 的取值范围是____________(答: 的取值范围是____________(答: ); );
(4)已知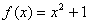 , ,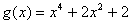 ,设 ,设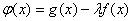 ,试问是否存在实数 ,试问是否存在实数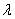 ,使 ,使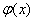 在 在 上是减函数,并且在 上是减函数,并且在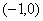 上是增函数?(答: 上是增函数?(答: ) )
(2)利用导数求函数单调区间的步骤:(1)求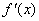 ;(2)求方程 ;(2)求方程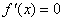 的根,设根为 的根,设根为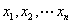 ;(3) ;(3)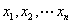 将给定区间分成n+1个子区间,再在每一个子区间内判断 将给定区间分成n+1个子区间,再在每一个子区间内判断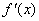 的符号,由此确定每一子区间的单调性。 的符号,由此确定每一子区间的单调性。
如设函数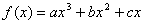 在 在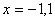 处有极值,且 处有极值,且 ,求 ,求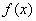 的单调区间。(答:递增区间(-1,1),递减区间 的单调区间。(答:递增区间(-1,1),递减区间 ) )
7、函数的极值:
(1)定义:设函数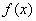 在点 在点 附近有定义,如果对 附近有定义,如果对 附近所有的点,都有 附近所有的点,都有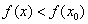 ,就说是 ,就说是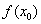 函数 函数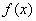 的一个极大值。记作 的一个极大值。记作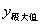 = =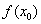 ,如果对 ,如果对 附近所有的点,都有 附近所有的点,都有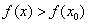 ,就说是 ,就说是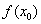 函数 函数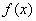 的一个极小值。记作 的一个极小值。记作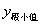 = =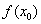 。极大值和极小值统称为极值。 。极大值和极小值统称为极值。
(2)求函数 在某个区间上的极值的步骤:(i)求导数 在某个区间上的极值的步骤:(i)求导数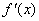 ;(ii)求方程 ;(ii)求方程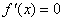 的根 的根 ;(iii)检查 ;(iii)检查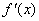 在方程 在方程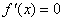 的根 的根 的左右的符号:“左正右负” 的左右的符号:“左正右负”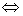  在 在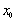 处取极大值;“左负右正” 处取极大值;“左负右正”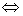  在 在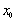 处取极小值。特别提醒: 处取极小值。特别提醒:
① 是极值点的充要条件是 是极值点的充要条件是 点两侧导数异号,而不仅是 点两侧导数异号,而不仅是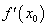 =0, =0,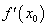 =0是 =0是 为极值点的必要而不充分条件。 为极值点的必要而不充分条件。
②给出函数极大(小)值的条件,一定要既考虑 ,又要考虑检验“左正右负”(“左负右正”)的转化,否则条件没有用完,这一点一定要切记! ,又要考虑检验“左正右负”(“左负右正”)的转化,否则条件没有用完,这一点一定要切记!
如(1)函数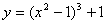 的极值点是 A、极大值点 的极值点是 A、极大值点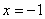 B、极大值点 B、极大值点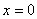 C、极小值点 C、极小值点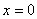 D、极小值点 D、极小值点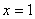 (答:C);(2)已知函数 (答:C);(2)已知函数 有极大值和极小值,则实数 有极大值和极小值,则实数 的取值范围是_____(答: 的取值范围是_____(答: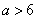 或 或 );(3)函数 );(3)函数 处有极小值10,则a+b的值为____(答:-7);(4)已知函数 处有极小值10,则a+b的值为____(答:-7);(4)已知函数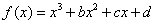 在区间[-1,2 ]上是减函数,那么b+c有最___值___(答:大, 在区间[-1,2 ]上是减函数,那么b+c有最___值___(答:大,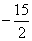 ) )
8、函数的最大值和最小值:
(1)定义:函数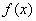 在一闭区间上的最大值是此函数在此区间上的极大值与其端点值中的“最大值”;函数 在一闭区间上的最大值是此函数在此区间上的极大值与其端点值中的“最大值”;函数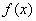 在一闭区间上的最小值是此函数在此区间上的极小值与其端点值中的“最小值”。 在一闭区间上的最小值是此函数在此区间上的极小值与其端点值中的“最小值”。
(2)求函数 在[ 在[ ]上的最大值与最小值的步骤:(1)求函数 ]上的最大值与最小值的步骤:(1)求函数 在( 在( )内的极值(极大值或极小值);(2)将 )内的极值(极大值或极小值);(2)将 的各极值与 的各极值与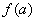 , ,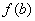 比较,其中最大的一个为最大值,最小的一个为最小值。 比较,其中最大的一个为最大值,最小的一个为最小值。
如(1)函数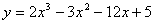 在[0,3]上的最大值、最小值分别是______(答:5; 在[0,3]上的最大值、最小值分别是______(答:5;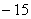 );(2)用总长14.8m的钢条制作一个长方体容器的框架,如果所制作容器的底面的一边比另一边长0.5m。那么高为多少时容器的容积最大?并求出它的最大容积。(答:高为1.2米时,容积最大为 );(2)用总长14.8m的钢条制作一个长方体容器的框架,如果所制作容器的底面的一边比另一边长0.5m。那么高为多少时容器的容积最大?并求出它的最大容积。(答:高为1.2米时,容积最大为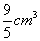 ) )
特别注意:(1)利用导数研究函数的单调性与最值(极值)时,要注意列表!(2)要善于应用函数的导数,考察函数单调性、最值(极值),研究函数的性态,数形结合解决方程不等式等相关问题。比如:
(1)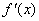 是 是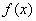 的导函数, 的导函数,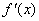 的图象如右图所示,则 的图象如右图所示,则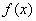 的图象只可能是 ( 答:D ) 的图象只可能是 ( 答:D )

(2)方程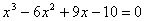 的实根的个数为______(答:1); 的实根的个数为______(答:1);
(3)已知函数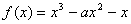 ,抛物线 ,抛物线 ,当 ,当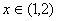 时,函数 时,函数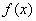 的图象在抛物线 的图象在抛物线 的上方,求 的上方,求 的取值范围(答: 的取值范围(答: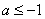 )。 )。
(责任编辑:admin) |
 ;(3)若
;(3)若
