湖南岳阳县七中 胡旭光供稿
一.选择题(5 10分) 10分)
1.已知 且 且 为真,则下列命题中真命题的个数为 为真,则下列命题中真命题的个数为
① ; ② ; ②  ; ③ ; ③ 或 或 ; ④非 ; ④非
(A) 1 (B)2 (C)3 (D)4
2.若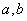 是两条异面直线,且分别在平面 是两条异面直线,且分别在平面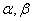 内,若 内,若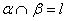 ,则直线 ,则直线 必定 必定
(A) 分别与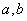 相交 (B) 至少与 相交 (B) 至少与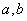 之一相交 (C) 与 之一相交 (C) 与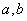 都不相交 (D) 至多与 都不相交 (D) 至多与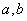 之一相交 之一相交
3.已知直线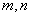 和平面 和平面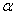 ,则 ,则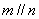 的一个必要不充分条件是 的一个必要不充分条件是
(A) 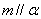 , ,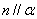 (B) (B)  , , (C) (C) 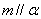 , ,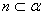 (D) (D) 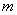 、 、 与 与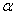 成等角 成等角
4.下列四个极限运算中,正确的是
(A)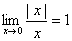 (B) (B) 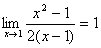 (C) (C)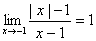 (D) (D)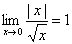
5.已知异面直线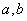 所成角为 所成角为 ,经过一点可以作多少条与 ,经过一点可以作多少条与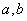 都成角为 都成角为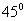 的直线 的直线
(A) 1 (B) 2 (C) 3 (D) 4
6.设 表示三条直线, 表示三条直线, 、 、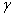 表示两个平面则下列命题中逆命题不成立的是 表示两个平面则下列命题中逆命题不成立的是
(A) 已知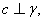 若 若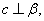 则 则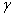 ∥ ∥ (B) 已知 (B) 已知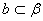 , , 是 是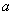 在 在 内的射影, 若 内的射影, 若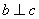 , 则 , 则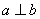
(C) 已知 , , ,若 ,若 ∥ ∥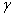 , 则 , 则 ∥ ∥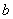 (D)已知 (D)已知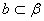 ,若 ,若 则 则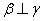
7.在直角坐标平面中,若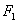 、 、 为定点, 为定点,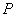 为动点, 为动点,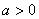 为常数,则“ 为常数,则“ ” 是“点 ” 是“点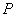 的轨迹是以 的轨迹是以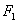 、 、 为焦点,以 为焦点,以 为长轴的椭圆”的 为长轴的椭圆”的
(A)充要条件 (B)仅必要条件 (C)仅充分条件 (D)非充分且非必要条件
8.过抛物线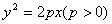 的焦点作直线交抛物线于 的焦点作直线交抛物线于 , ,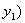 、 、 , , 两点,若 两点,若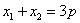 ,则 ,则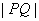 等于 等于
(A) 4 (B) 5 (B) 5 (C) 6 (C) 6 (D) 8 (D) 8
9.在正方体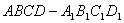 中, 中,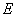 为 为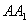 的中点,点 的中点,点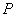 在其对角面 在其对角面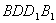 内运动,若 内运动,若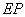 总与直线 总与直线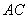 成等角,则点 成等角,则点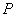 的轨迹有可能是 的轨迹有可能是
(A)圆或圆的一部分 (B)抛物线或其一部分 (C) 双曲线或其一部分 (D) 椭圆或其一部分
10.设函数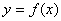 的定义域是 的定义域是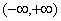 ,若对于任意的正数 ,若对于任意的正数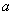 ,函数 ,函数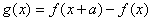 都是其定义域上的减函数,则函数 都是其定义域上的减函数,则函数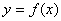 的图象可能是 的图象可能是
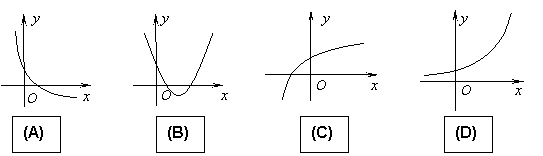
二.填空题(5 5分) 5分)
11.双曲线 的离心率 的离心率 ,则 ,则 的值为 . 的值为 .
12.函数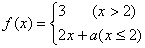 在 在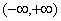 上处处连续,则常数 上处处连续,则常数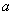 等于 . 等于 .
13.若两直线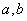 在平面 在平面 上的射影 上的射影 , , 是平行的直线,则 是平行的直线,则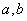 的位置关系是 . 的位置关系是 .
14.如果把圆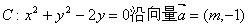 平移后得到圆 平移后得到圆 ,且 ,且 与直线 与直线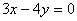 相切,则 相切,则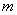 的值为 . 的值为 .
15.设有四个条件:
①平面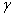 与平面 与平面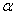 、 、 所成的锐二面角相等; 所成的锐二面角相等;
②直线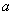 // //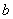 , ,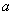 ⊥平面 ⊥平面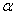 , ,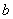 ⊥平面 ⊥平面 ; ;
③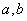 是异面直线, 是异面直线,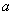 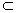 平面 平面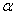 , ,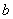 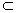 平面 平面 ,且 ,且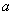 // // , ,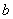 // //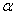 ; ;
④平面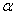 内距离为 内距离为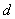 的两条平行直线在 的两条平行直线在 内的射影仍为两条距离为 内的射影仍为两条距离为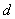 的平行线. 的平行线.
其中能推出平面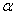 //平面 //平面 的条件有 (填写所有正确条件的代号) 的条件有 (填写所有正确条件的代号)
三.解答题(10+12+12+13+14+14分)
16.已知向量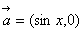 , ,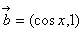 ,其中 ,其中 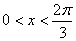 ,求 ,求 的取值范围. 的取值范围.
17.如图正方体在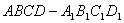 中, 中,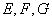 分别为 分别为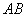 , ,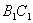 , , 的中点. 的中点.
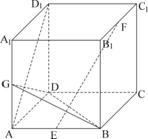
(1)求证: ⊥平面 ⊥平面 ; ;
(2)求异面直线 与 与 所成的角. 所成的角.
18.已知数列 的前 的前 项和为 项和为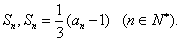
(1)求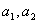 ; ;
(2)求数列 的通项. 的通项.
19.已知 是函数 是函数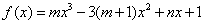 的一个极值点,其中 的一个极值点,其中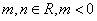 , ,
(1)求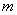 与 与 的关系式; 的关系式;
(2)求 的单调区间; 的单调区间;
(3)若 ,求证:函数 ,求证:函数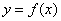 的图象与 的图象与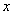 轴只有一个交点. 轴只有一个交点.
20.定义:离心率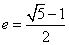 的椭圆为“黄金椭圆”.已知椭圆E: 的椭圆为“黄金椭圆”.已知椭圆E: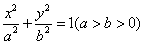 的一个焦点为 的一个焦点为 ( (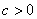 ), ),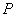 为椭圆 为椭圆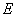 上的任意一点. 上的任意一点.
(1)试证:若 不是等比数列,则 不是等比数列,则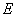 一定不是“黄金椭圆”; 一定不是“黄金椭圆”;
(2)设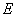 为“黄金椭圆”,问:是否存在过点 为“黄金椭圆”,问:是否存在过点 、 、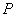 的直线 的直线 与 与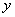 轴的交点 轴的交点 满足 满足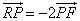 ?若存在,求直线 ?若存在,求直线 的斜率 的斜率 ;若不存在,说明理由. ;若不存在,说明理由.
(3)已知椭圆E的短轴长是2, 点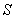 (0,2), 求使 (0,2), 求使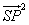 取最大值时点 取最大值时点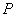 的坐标. 的坐标.
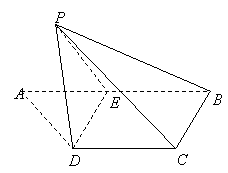
21.如图,梯形 中, 中, , ,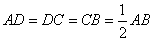 , ,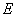 是 是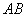 的中点,将 的中点,将 沿 沿 折起,使点 折起,使点 折到点 折到点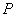 的位置,且二面角 的位置,且二面角 的大小为 的大小为
(1)求证: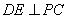 ; ;
(2)求直线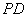 与平面 与平面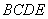 所成角的大小; 所成角的大小;
(3)求点 到平面 到平面 的距离. 的距离.
(附加题15分,不计入总分)
22.对于定义域为 的函数 的函数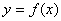 ,若同时满足下列条件: ,若同时满足下列条件:
① 在 在 内单调递增或单调递减; 内单调递增或单调递减;
②存在区间[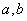 ] ]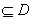 ,使 ,使 在[ 在[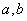 ]上的值域为[ ]上的值域为[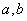 ];那么把 ];那么把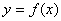 ( (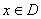 )叫闭函数. )叫闭函数.
(1)求闭函数 符合条件②的区间[ 符合条件②的区间[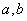 ]. ].
(2)判断函数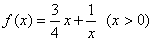 是否为闭函数?并说明理由. 是否为闭函数?并说明理由.
(3)若 是闭函数,求实数 是闭函数,求实数 的取值范围. 的取值范围.
(责任编辑:admin) |