|
湖南省常德市安乡县第五中学 龚光勇收集整理 基本概念、公式及方法是数学解题的基础工具和基本技能，为此作为临考前的高三学生，务必首先要掌握高中数学中的概念、公式及基本解题方法，其次要熟悉一些基本题型，明确解题中的易误点，还应了解一些常用结论，最后还要掌握一些的应试技巧。本资料对高中数学所涉及到的概念、公式、常见题型、常用方法和结论及解题中的易误点，按章节进行了系统的整理，最后阐述了考试中的一些常用技巧，相信通过对本资料的认真研读，一定能大幅度地提升高考数学成绩。 1.集合元素具有确定性、无序性和互异性. 在求有关集合问题时，尤其要注意元素的互异性。 举例如下： （1）设P、Q为两个非空实数集合，定义集合P+Q=  ，若 ， ，则P+Q中元素的有________个。（答：8）（2）设  ， ，  ，那么点 的充要条件是________（答： ）；（3）非空集合  ，且满足“若 ，则 ”，这样的 共有_____个（答：7）2.遇到  时，你是否注意到“极端”情况： 或 ；同样当 时，你是否忘记的情形？要注意到 是任何集合的子集，是任何非空集合的真子集。举例如下： 集合  ， ，且 ，则实数 ＝______.（答： ）3.对于含有  个元素的有限集合 ，其子集、真子集、非空子集、非空真子集的个数依次为   。举例如下： 满足  集合M有______个。 （答：7）4.集合的运算性质： ⑴  ； ⑵ ；⑶  ； ⑷ ； ⑸ ； ⑹  ；⑺ 。举例如下： 如设全集  ，若 ， ， ，则A＝_____，B＝___.（答： ， ）5. 研究集合问题，一定要理解集合的意义――抓住集合的代表元素。如：  —函数的定义域； —函数的值域； —函数图象上的点集。举例如下： （1）设集合  ，集合N＝ ，则 ___（答： ）；（2）设集合  ， ， ，则 _____（答： ） 6. 数轴和韦恩图是进行交、并、补运算的有力工具，在具体计算时不要忘了集合本身和空集这两种特殊情况，补集思想常运用于解决否定型或正面较复杂的有关问题。 举例如下： 已知函数  在区间 上至少存在一个实数 ，使 ，求实数 的取值范围。 （答： ）7.复合命题真假的判断。“或命题”的真假特点是“一真即真，要假全假”；“且命题”的真假特点是“一假即假，要真全真”；“非命题”的真假特点是“真假相反”。 举例如下： 在下列说法中： ⑴“ 且 ”为真是“或”为真的充分不必要条件；⑵“ 且”为假是“或”为真的充分不必要条件；⑶“ 或”为真是“非”为假的必要不充分条件；⑷“非 ”为真是“且”为假的必要不充分条件。其中正确的是__________（答：⑴⑶）8.四种命题及其相互关系。若原命题是“若p则q”，则逆命题为“若q则p”；否命题为“若﹁p 则﹁q” ；逆否命题为“若﹁q 则﹁p”。 提醒： （1）互为逆否关系的命题是等价命题，即原命题与逆否命题同真、同假；逆命题与否命题同真同假。但原命题与逆命题、否命题都不等价； （2）在写出一个含有“或”、“且”命题的否命题时，要注意“非或即且，非且即或”； （3）要注意区别“否命题”与“命题的否定”：否命题要对命题的条件和结论都否定，而命题的否定仅对命题的结论否定； （4）对于条件或结论是不等关系或否定式的命题，一般利用等价关系“  ”判断其真假，这也是反证法的理论依据。（5）哪些命题宜用反证法？如（1）“在△ABC中，若∠C=900，则∠A、∠B都是锐角”的否命题为 （答：在  中，若 ，则 不都是锐角）；（2）已知函数 ，证明方程 没有负数根。9.充要条件。关键是分清条件和结论（划主谓宾），由条件可推出结论，条件是结论成立的充分条件；由结论可推出条件，则条件是结论成立的必要条件。从集合角度解释，若  ，则A是B的充分条件；若 ，则A是B的必要条件；若A=B，则A是B的充要条件。比如：（1）给出下列命题：①实数  是直线 与 平行的充要条件；②若 是 成立的充要条件；③已知 ，“若 ，则 或 ”的逆否命题是“若 或 则 ”；④“若和 都是偶数，则 是偶数”的否命题是假命题 。其中正确命题的序号是_______（答：①④）；（2）设命题p：  ；命题q: 。若┐p是┐q的必要而不充分的条件，则实数a的取值范围是 （答： ）10. 一元一次不等式的解法：通过去分母、去括号、移项、合并同类项等步骤化为  的形式，若 ,则 ；若 ,则 ；若 ,则当 时， ；当 时， 。如已知关于  的不等式 的解集为 ，则关于的不等式 的解集为_______（答： ）11. 一元二次不等式的解集（联系图象）。尤其当  和 时的解集你会正确表示吗？设, 是方程 的两实根，且 ，则其解集如下表：
如解关于 的不等式： 。（答：当时， ；当时，或 ；当 时， ；当 时，；当 时， ）12. 对于方程  有实数解的问题。首先要讨论最高次项系数是否为0，其次若 ，则一定有 。对于多项式方程、不等式、函数的最高次项中含有参数时，你是否注意到同样的情形？比如：（1）  对一切 恒成立，则的取值范围是_______（答： ）；（2）关于 的方程 有解的条件是什么？(答： ，其中 为 的值域)，特别地，若在 内有两个不等的实根满足等式 ，则实数 的范围是_______.（答： ）13.一元二次方程根的分布理论。方程  在 上有两根、在 上有两根、在 和上各有一根的充要条件分别是什么？（  、  、 ）。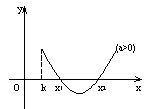根的分布理论成立的前提是开区间，若在闭区间 讨论方程 有实数解的情况，可先利用在开区间上实根分布的情况，得出结果，再令 和 检查端点的情况．如实系数方程  的一根大于0且小于1，另一根大于1且小于2，则 的取值范围是_________（答：（ ，1））14.二次方程、二次不等式、二次函数间的联系你了解了吗？二次方程 的两个根即为二次不等式 的解集的端点值，也是二次函数 的图象与轴的交点的横坐标。比如：（1）不等式  的解集是 ，则=__________（答： ）；（2）若关于 的不等式 的解集为 ，其中 ，则关于的不等式 的解集为________（答： ）；（3）不等式  对 恒成立，则实数的取值范围是_______（答：）。(责任编辑：admin) |
或
或
