|
溧阳南渡高级中学 辛春 数学是研究空间形式和数量关系的科学，而数形结合思想是一种很重要的数学思想，正是基于对数与形的抽象研究才产生了数学这门学科，才能使人们能够从不同侧面认识事物。华罗庚先生说过:“数与形本是两依倚,焉能分作两边飞. 数缺形时少直观, 形少数时难入微.”.把数量关系的研究转化为图形性质的研究，或者把图形性质的研究转化为数量关系的研究，这种解决问题过程中“数”与“形”相互转化的研究策略，就是数形结合的思想。 在使用的过程中，由“形”到“数”的转化，往往比较明显，而由“数”到“形”的转化却需要转化的意识，因此，对数形结合的呈现形式及转化时应注意的问题加以研究才能更好地进行数与形的转化。 一 数中构形 把数学问题的数量信息转换为图形信息，由图形的特征的启示抓住问题的本质，寻找解决问题的途径。 【例1】（2005年, 辽宁卷)一给定函数 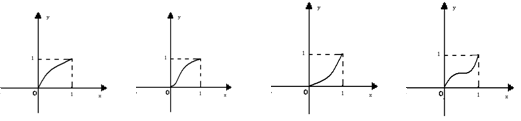 的图象在下列图中，并且对任意 ，由关系式 得到的数列 满足 ，则该函数的图象是（ ） （A） （B） （C） （D） 【分析及解】这是一道函数,数列,函数图象综合在一起的选择题,需要通过数列的性质研究函数图象的特征.实际上,只要设  ,则有且 ,并对所有 都成立,因此选(A). 【分析及解】本题大部分考生都是用三角恒等变形和正弦定理通过一定量的计算来完成,但是注意到数形结合,可以很快解决问题.为此,延长 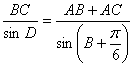 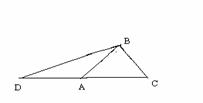到 ,使 ,则  ,  由正弦定理  ,即 ,由此,选(C). 二 形中思数 由形思数，把空间形式进行代数化处理，淡化传统的“由形到形”的几何推理，用数量关系刻画事物的本质特征，从而探幽发微。 【例3】（2006年湖南卷，理）若圆  上至少有三个不同的点到直线 的距离为 ,则直线 的倾斜角的取值范围是（A）  （B） （C） （D） 【分析及解】 圆 整理为 ，∴圆心坐标为(2，2)，半径为3 ，要求圆上至少有三个不同的点到直线的距离为，则圆心到直线的距离应小于等于， ∴  ，∴  ，∴  ， ，∴  ，直线的倾斜角的取值范围是，选B.【例4】(2006年辽宁卷，理)直线  与曲线  的公共点的个数为(A)1 (B)2 (C)3 (D)4 【分析及解】将 代入得：  ，显然该关于 的方程有两正解，即x有四解，所以交点有4个，故选择答案D。 (责任编辑：admin) |