|
广东省吴川市振文中学 柯厚宝 立几问题是考查空间想象能力的主要素材，但是由于学生的认识水平、思维水平与平时训练不得法等原因，造成了不少同学对立几问题产生了一种画不出、摸不着、看不到的感觉.下面我们从构建几个典型模型入手，突破这一难点. 1 构建正方体模型解题 例1 关于直线m、n与平面  ,有下列四个命题：①若m//α,n//β且α//β,则m//n； ②若m  α,n//β且 ,则 ；③若m α,n//β且α//β,则；④若m//α,n β且,则m//n..其中真命题的序号是（ ） (A)①、② (B)③、④ (C)①、④ (D)②、③ 分析：本题的平行与垂直量较多，可构建正方体模型，将它们置于正方体中进行考虑. 解：构建如图1所示的正方体，设  为平面EFGH， 为平面ABCD，m为AB，n为FG，则①不正确；设 为平面EFGH，为平面FGCB，m为AE，n为DH，知②不正确，同理知③、④正确，选B. 点评：据题意构建适宜的模型，使得解题更直观、更具操作性. 例2 用6根长度为1的铁棍焊接成一个正四面体框架，若忽略铁棍的粗细，则该框架能够容纳得下的最大球体的半径为 . 分析：直接计算运算量较大，从整体考虑，我们可构建正方体模型进行求解. 解：构建如图2所示的正方体，把焊接成的正四面体框架放置于其中，则球心为正方体的中心，最大球体的半径为正方体中心到对角线AB中点的距离，另一方面，由AB=1，得正方体的棱长为  ，正方体中心到AB中点的距离为 ，于是最大球体的半径为. 点评：熟悉基本模型，为寻找立几问题的解题入口及巧解问题提供了基础. 2 构建长方体模型解题 例3 山坡与水平面成  角，坡面上有一条与山底坡脚的水平线成的直线小路，某人沿小路上坡走了一段路后升高了100m,则此人走了（ ）(A)300m (B)400m (C)200m (D)  m分析：题中给出了具体的二面角与线线所成的角，可构建长方体模型把关系理清， 进而求解. 解：构建如图3所示的长方体，设平面ABD为坡面，平面ABC为水平面，AD为小路，AB为水平线,则 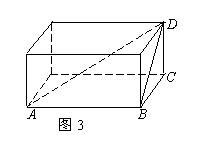 ， ，CD=100m,于是BD=2CD=200m，AD=2BD=400m,选B. 点评：构建模型，易于我们从整体的高度把握住问题的本质. 例4 某人做了一个对棱相等的四面体，它们的长度分别为5、6、7，则这个四面体的体积等于 . 分析：若按常规思路，这问题的解答很繁.而在长方体中，存在一个对棱相等的四面体，于是可把它放到长方体中进行求解. 解：构建如图4所示的长方体,设AD=BC=5,AB=CD=6,AC=BD=7,EA=a,EB=b,ED=c,则  ，解得 ， ， ，∴  . 点评：若四面体是对棱相等的四面体，则它外接于一个长方体，四面体的体积是外接长方体体积的  .3 构建回路向量模型解题 我们称  为回路向量，变形有 ，并可作推广.这结果貌似简单，实熟好用.例5若异面直线  所成的角为 ,AB是公垂线,E,F分别是异面直线上到A,B距离为2和1的两点,当 时,线段AB的长为 .分析：本题有  ，于是可构建回路向量求解.解:如图5, 由  ,得 (1)当  时,有 ,得 ;(2)当  时,有 ,得 .故答案为 或 . 点评：构建回路向量求解，避免了繁杂的直线平移与辅助线的添加，使解题一目了然. 4 构建函数模型解题 例6请您设计一个帐篷.它下部的形状是高为1m的正六棱柱,上部的形状是侧棱长为3m的正六棱锥（如右图所示）.试问当帐篷的顶点O到底面中心O1的距离为多少时，帐篷的体积最大？ 分析：本题涉及变量与最值问题，可构建函数模型求解.
解：设底面的正六边形的边长为  ，则正六棱锥的高为 ，正六边形的面积为 ，则帐篷的体积为 =  令  ，则 ，有 ， ，令 ，得 （舍去）或 ,当  时， ， 为增函数；当 时， ，为减函数.∴当 时，取得最大值， 也取得最大值，这时 .答：当OO1为2m时，帐篷的体积最大. 点评：函数方法是处理变量与定值（最值）的有力工具，构建函数模型，可将问题放到函数的大环境中进行考虑，使得解题自然流畅. 除以上模型外，还可构建坐标模型解题，由于这方面的探讨在教辅资料中已较为丰富，这里不再赘述. (责任编辑：admin) |
