|
厦门市前埔厦门特殊教育学校 吴光安 在高中阶段，有一个公式一直让我产生兴趣，就是  ，这个公式是学习数学归纳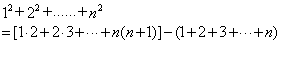法的时候，课后的一个习题结论，而且也是老教材的封面的内容，可见该公式是多么的重要，不然怎么会上了封面呢。的确在实际的解题中，该公式是很有用的：直接用这个公式，可以使一些过程变得很简单。但老师讲到这的时候，叫我们只要记住结论就可以了，虽然可以这样，但它的证明方法却一直让我产生兴趣。在学习的过程中，我发现了6种证明方法：方法一： 直接求出  的和比较难，可以采用代数的方法，为了找出 的代数表达式，用 去探索由于  可得：  现在关键是求出：  而： = 于是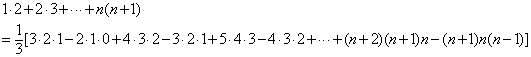：   所以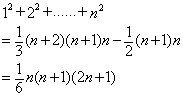：  方法二： 学习了排列与组合的知识，知道有  ，从而可得： = 于是：  同时有结论：  = = 于是有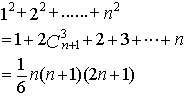：  方法三： 拿到了题目，不知如何下手，于是只好在草稿上写出前几项的和，细心点，嘿！发现有  = ，于是易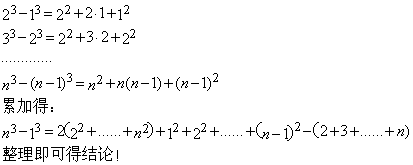得结论！方法四：  方法五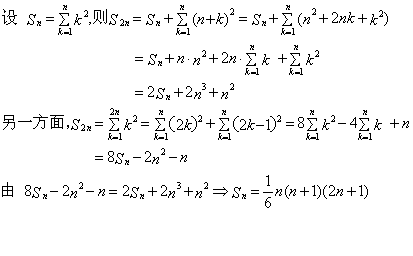：  方法六： 用数学归纳法。 总结： 方法一思路较简单，而且这种方法具有“移植性”，比如要求  则可以类似 ，而  ”的角度来求出它的值（当然关于完全可以用观察法来解决）方法二用到了排列组合中的知识： ，=，对于高中生而言，这部分是比较陌生的，遇到这种题目的时候，往往会有畏惧情绪，但高考题却经常会涉及，比如说2003年的一道选择题，又如2001年的考题： 据说当时很多人看到这题目就傻眼了，如果平时能象证明上述公式那样多用偏僻的知识思考问题，那遇到这种高考题的时候，也更从容了。 方法三是数学中常用的方法，其实数学中很多结论都是在“尝试”下生成的，关键是观察能力要强，我认为这种方法对于新课改具有重要意义，这样可以培养学生发现知识的能力。 方法四是在学习“数列”时常用的方法，一定要活学活用这种方法。 方法五显得有些不自然，似乎有些深奥，但如果多用这种语言来解题，思维能力肯定可以提高，以后在学习微积分的级数的时候，可能会觉得轻松点。 (责任编辑：admin) |