|
贵州省黄平县旧州中学 杨胜万 人教版新教材高一数学(第一册下)在给出平面向量数量积的性质中，有这样一条性质：  在上述性质中,若设  ， ，则由向量数量积的坐标表示，可变形为： (其中等号成立的条件是 与 共线或 )利用上述性质及其变形，有时可简捷地解决与不等式有关的其它数学问题。下面试举几例加以说明其应用： 1、证明不等式 例1 已知a、b是不相等的两个正数，求证：  （新人教版高中数学第二册上 习题6.3第6题）证明：构造向量  ， ，则由a、b为不相等的两个正数可知：向量、不共线。此时此时有： ，而  ， ，从而有：  ，也即： 例2 求证：  （高中数学第二册上 练习第3题）证明：构造向量  ， ，则向量、不相等，至多反向。因为 ， ，由 得： ， ，又向量、不相等 ，所以。2、证明恒等式或求值 例3 已知：  且 ，则 （第三届希望杯全国数学邀请赛试题）证明：构造向量  ， ，由得： ，易知上式中等号成立，所以 ，从而例4 在锐角  中，已知 ，求角C的值。解：由 ，得： 构造向量  ， ，由，得： 化简整理得：  ，所以 ，又 ，从而 由不等式取等号条件知  ，故而 3、求值域或最值 例5 求函数 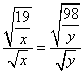 的最大值。解：设  ， ，则 ， ，由得： ，当且仅当  且方向相同时，不等式取“=”号，即： ，解之得： 所以当 时， 例6 设  且 ，求 的最小值。（1998年湖南省高中数学竞赛题）设向量  ， ，则 ， ，并且 ，由得： ，所以 ，当且仅当、同向即 ，解得： 时不等式取等号，故的最小值为 4、解方程（组） 例7 解方程  解：因为  ，方程两边同除以 ，得； 设  ， ，由得： 所以上式中等号成立，从而有  解之得：  代入原方程检验均适合。 5、解其它问题 利用平面向量的性质 及其变形，除了可以解决上述问题外，还可以解决诸如数列等其它相关问题，从上述各例来看，利用该性质来解决问题，关键是将条件式如何转化为向量的坐标表示，然后才能套用公式求解（或求证），特别注意的是在求最值时还注意等号成立的条件。(责任编辑：admin) |