|
山东省临清市第二中学 马英济 本文试图区别于新课标教材，采用起点更低，更易于学生接受的思路与方法，进行三角恒等变换的入门教学。由特殊到一般，利用合情推理的方式研究倍角公式、和角公式，对学生数学思维训练更有价值。 诱思探究 如何用sinα,cosα 表示sin2α,cos2α 呢?可作如下尝试: 一.关于  、 的推证   如图构造等腰△ABC,过A作AD垂直于BC,垂足为D.过B作BE垂直于CA,垂足为E.设∠BAC=2  ,AB=AC=1. 则AD=cosα，BD=DC=sinα,BE=sin2α （如图（1）） 或 BE=sin（π-2α）＝sin2α（如图（2））考虑△ABC的面积，有  即  于是，  （）接下来寻求 的推证如图（1）AE= cos2α. 又等腰△ABC中,  . EC=BCcosC= AE=AC-EC=  ,  即  = ()如图（2）AE=  ,EC=BCcosC= 又EC=AE+AC=  , ∴ ＝ 于是  （）诱思探究: 能否推证Sα+β呢?可作如下尝试: 二.关于Sα+β的推证 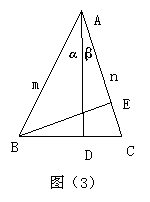  如图构造△ABC，设AB=m , AC=n . AD⊥BC ,D为垂足，∠BAD=α，∠DAC=β,过B作BE⊥CA,E为垂足.则 BE=msin(α+β)  , . 即   (Sα+β)说明:通过构造三角形,利用直角三角形中的锐角三角函数和三角形的面积公式.推证S2α ,Sα+β.上面的结果是在α,β都是锐角的情况下得到的.对于α,β都是任意角的情形,有兴趣的同学可用诱导公式自己推证,在此不在赘述. 三角恒等变换的学习以代数变换为基础,考虑变换的对象,变换的目标以及变换的依据,加上公式之间存在的必然的紧密的内在联系,从一个公式入手,层层展开,就能形成和谐统一的三角公式体系. (责任编辑：admin) |