甘肃省武威六中 陈怀发
数学是研究客观世界的数量关系和空间形式的科学,数和形是数学研究的两个重要方面,在研究过程中,数形结合既是一个重要的数学思想,又是一种常用的数学方法。华罗庚先生曾指出:“数缺形时少直观,形少数时难入微。数形结合百般好,隔裂分家万事休。”
数形结合包括“以形助数”和“以数辅形”两个方面,高中阶段用的较多的是以形助数,高考中时有出现,在选择、填空题的解答中更能体现其优越性,近年在解答题中也加重了对数形结合的考查。 本文仅就以形助数解决代数问题做粗略的探讨。
在代数问题的解决中,许多数量关系的抽象概念和解析式,若赋予其几何意义,往往变得非常直观形象,从而使问题简单化,达到事半功倍优化解题途径的目的,这种“数”与“形”的信息转换,相互渗透,不仅可以使一些题目的解决简捷明快,同时还可以大大开拓我们的解题思路。
1.以形助数解决代数问题的途径:
1.1 通过坐标系。如直角坐标系中,由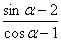 可联想到两点连线的斜率。 可联想到两点连线的斜率。
由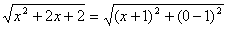 可想到两点间距离。复平面中 可想到两点间距离。复平面中 为复数所对应的两点间的距离。 为复数所对应的两点间的距离。
1.2 转化。把正数a看成距离,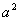 (或ab)看成面积, (或ab)看成面积,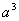 或(abc)看成体积, 或(abc)看成体积,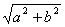 看成勾股定理, 看成勾股定理,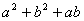 与余弦定理相联系。 与余弦定理相联系。
1.3 构造。构造一个几何图形,或构造函数.
2、以形助数解决的几类问题
2.1 以形助数求最值
例1:求函数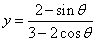 的最大值和最小值 的最大值和最小值
分析:如图1,本题是求三角函数的最值,现联想在直角坐标平面xoy上,引入点P(3,2),Q(2cos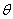 ,sin ,sin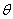 )则Q点的轨迹是椭圆: )则Q点的轨迹是椭圆:  ,而y是直线PQ的斜率,由图知直线PQ和椭圆相切时斜率取得最大和最小值,于是三角函数问题在平面解析几何中得到解决。 ,而y是直线PQ的斜率,由图知直线PQ和椭圆相切时斜率取得最大和最小值,于是三角函数问题在平面解析几何中得到解决。
解:设直线的方程为: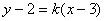
即: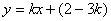
由相切的充要条件得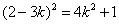
解得 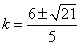 ∴ ∴

2.2 以形助数求方程解的个数。
例2:当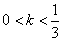 时,关于 时,关于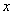 的方程 的方程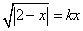 有几个实根? 有几个实根?
分析:如图2,令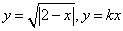 。则方程 。则方程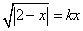 的实根个数等价于方程组 的实根个数等价于方程组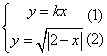 的解的个数。方程(2)可化为 的解的个数。方程(2)可化为 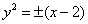 ( ( ),它表示两条抛物线的上半支,故只要求出射线 ),它表示两条抛物线的上半支,故只要求出射线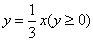 与它们的交点个数即可。易知交点有三个。故当 与它们的交点个数即可。易知交点有三个。故当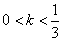 时,关于 时,关于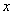 的方程 的方程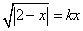 有三个实根。 有三个实根。

此类题目若用代数法求解非常繁杂,而用解析法却如此简单,其关键还是曲线与直线方程的构造及曲线与直线关系的应用较为直观、简便。
2.3 以形助数解、证不等式。
例3 设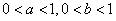 ,求证: ,求证: 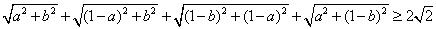
分析:如图3,在直角坐标系中,构造单位正方形,四顶点分别为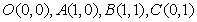 ,由于 ,由于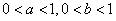 ,因此可在正方形内任取一点 ,因此可在正方形内任取一点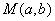 ,于是这一看似与几何图形不相关的问题的就转化为证明点M到正方形四顶点的距离之和不小于 ,于是这一看似与几何图形不相关的问题的就转化为证明点M到正方形四顶点的距离之和不小于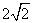 的问题。 的问题。
证明: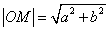 , ,
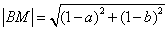
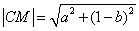
而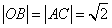
又∵ 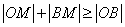 , ,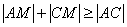
∴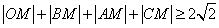
即 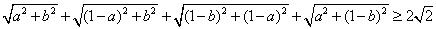
其中当M取对角线交点时等号成立。
2.4 以形助数求参数的范围。
例4.如果函数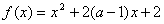 在区间 在区间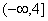 上是减函数,那么实数a的取值范围是( ) 上是减函数,那么实数a的取值范围是( )
(A)a≥-3 (B)a≤-3 (C)a≤5 (D)a≥3
[分析及解] 如图4 可画出f(x)的草图,对称轴为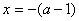 ,开口向上,若使函数在 ,开口向上,若使函数在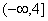 上是减函数,则区间 上是减函数,则区间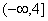 在对称轴的左侧,即 在对称轴的左侧,即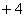 ≤ ≤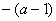 ,∴ ,∴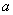 ≤-3.选B. ≤-3.选B.
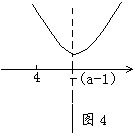
此题若不结合图形,只是按单调性的概念理解,则需利用单调性的定义去证,求解过程繁琐,特别对于一道选择题,就得不偿失了。
2.5 以形助数求代数式的值。
例6:求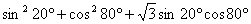 的值. 的值.
[分析及解]如图5,本题结构与余弦定理形式相似,联想构造三角形用余弦定理来解。

∵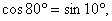 且 且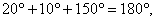 则以 则以 为内角构造一个三角形.设 为内角构造一个三角形.设 角的对边分别为 角的对边分别为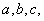 外接圆半径为R,则 外接圆半径为R,则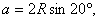 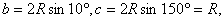 由余弦定理,得 由余弦定理,得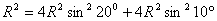 + +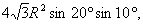 化简 化简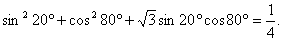
数形结合既具有数学学科的鲜明特点,又是数学研究的常用方法.纵观多年来的高考试题,利用数形结合思想解题比比皆是,因此在教学中应引导学生树立数形结合的思想, 以形助数巧解代数问题。
(责任编辑:admin) |


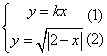 的解的个数。方程(2)可化为
的解的个数。方程(2)可化为