|
山东省胶南市第一中学 韩朝泉 一．平面向量基本定理中方程的应用技巧 设 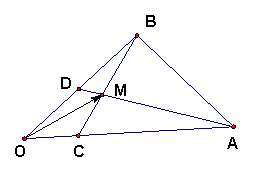 是平面内的两个不共线向量， 是平面内的任意一个向量，按照平面向量基本定理，  ，而且 是唯一确定的．可见，应用平面向量基本定理关键是确定，而方程（组）在确定系数方面具有无可替代的作用，解题时，将确定系数问题转化为方程（组）问题是一个常用技巧．例1．如图所示，在  中， ， 与 交于点Ｍ，设 ， ，试用 表求 ． 分析：由于点Ｍ是AD与BC两条线段的交点，Ｍ在这两条线段上的具体位置不能用数量表示，因此，直接用三角形法则，不能将 转化为用表示；这时，方程可以发挥重要作用，如果设  ，那么只需要依据A，Ｍ，D三点共线及B，Ｍ，C三点共线列出方程组即可得解．解析：设  ，则 ， ，由于A，Ｍ，D三点共线，所以   ；而  ， ，由于C，Ｍ，B三点共线，所以，  ；由  解得 ，所以， ．二．方程在向量的坐标运算中的应用技巧 方程在解决某些向量的坐标运算问题时，常可起到化繁为简的作用．主要用于确定向量的坐标、应用向量平行、垂直的坐标形式等． 例２．已知  且 求 ．分析：向量的坐标只与向量的起点，终点坐标有关，因此，只要求出点Ｍ和点Ｎ的坐标即可．根据条件 可以设出点Ｍ和点Ｎ的坐标，列出两个方程，通过解方程组得到点Ｍ和点Ｎ的坐标．解析：  ，  ；设  ，则 ，由 ，可得 ；即  ，同理可得 ．所以， ．三．解决向量中参数的有关计算问题 向量中有些含有参数的问题，在求参数的值，或求参数的范围时，方程起到至关重要的作用．由于参数一般存在于表达式中，因此，在形式上就给布列方程创造了条件，只需将含参数的表达式坐标化，即可得到所需方程（组）． 例３．已知  =4， ， ．(1)求 与 的夹角 ；(2)设  ，在线段 上是否存在点M，使 ，若存在，求出点M的坐标，若不存在，请说明理由．分析：（１）将 =4，代入已知的式子中，即可解出 的值，进而可以解出夹角；整个过程就是一个解方程的过程．（２）这是一个探索性的问题，可以假设存在这样的点M，由于点M在线段 上，为了确定点M的位置，可以引入参数 ，令 ，由的值确定点M的位置；这样，点M是否存在的问题就转化为参数是否存在的问题，将已知条件代入，即转化为方程是否有解的问题．解析：（１）  ， ，又因为 =4，，  ，即 ．（２）设存在点M，满足  ，则  ， ，解得 或  或 所以，存在点  或点 满足题意．(责任编辑：admin) |