|
根据解决问题的需要,常把数量关系的问题转化为图形的性质问题来讨论,即把抽象的“数”结构与形象的“形”结构联系起来,化抽象为直观,通过对图形的研究,常能发现问题的隐含条件,诱发解题线索,使求解过程变得简捷直观. (一)用几何法解代数问题 例11 已知正数a、b、c、A、B、C满足a+A=b+B=c+C=k.求证:aB+bC+cA<k2. 思路分析 不等式左边是二次三项式,联想到三角形的面积,可以构造以k为边长的正三角形PQR(如图12),在边上取L、M、N,根据已知条件,使QL=A,LR=a,RM=B,MP=b,PN=C,NQ=c.则 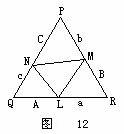  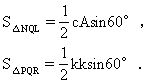 由图显见S△LRM+S△MPN+S△NQL<S△PQR. 即aB+bC+cA<k2. 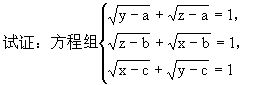 有唯一的一组解. 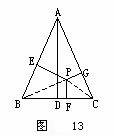 思路分析 由已知联想到:“等边三角形内任一点到三边的距离之和等于它的高(维维安尼定理).”所以作边长为1的等边三角形ABC,  =1(左边的两项刚好是垂足F分线段BC所成线段BF和FC的长,而BF+FC=BC=1). 同理,另两个方程也成立.再由作图知P唯一,故方程组的解唯一. (责任编辑:admin) |
