|
通过作图及利用图形的性质,将“数”的问题转化为“形”的问题,可使问题直观化、形象化.这种解题方法易于理解和掌握,能探求和检查解答的结果,还可避免复杂的计算与推导,有利于发展求异思维. 例25 已知方程x2+px+q=0① 有相异实根.求证:方程x2+px+q+k(2x+p)=0② 必有相异的实根,并且其中仅有一根在方程①的两根之间(其中k、p、q均为实数,且k≠0),  思路分析 证明方程②有相异实根,只须求证此方程根的判别式Δ2>0即可.而讨论根的分布情况就不那么简单了.以下借助图形进行探索: 设x1、x2是方程①的两个实根,且x1<x2.令f(x)=x2+px+q,则函数f(x)的图象开口向上,且与x轴交于(x1,0)、(x2,0)两点.设α、β是方程②的两个实根,α<β.令g(x)=x2+px+q+k(2x+p),则函数g(x)的图象开口向上,与x轴交于(α,0)、(β,0)两点.作函数图象,如结论成立,则四个根相互之间的关系有两种情况(如图13-24). 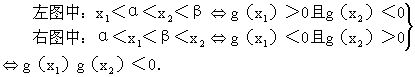 由此找到了简单的证明途径: g(x1)g(x2)=k2(2x1+p)(2x2+p) =k2[4x1x2+2p(x1+x2)+p2] =k2(4q+2p(-p)+p2] =k2(4q-p2)<0. 从而问题得证. 例26 设f(x)是定义在R上的周期为2的周期偶函数,已知当x∈[2,3]时,f(x)=x.求x∈[-2,0]时f(x)的解析式. 思路分析 先画出x∈[2,3]时f(x)的图象;再由周期性可画出f(x)在[0,1]和[-2,-1]上的图象,再由偶函数图象关于y轴对称的性质,可画出x∈[-3,-2]和x∈[-1,0]的图象(如图25).由图象不难求出 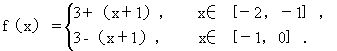 因此当x∈[-2,0]时,f(x)=3-|x+1|.  例27 已知n为自然数,实数a>1.解关于x的不等式 logax-4loga2x+12loga3x+…+n(-2)n-1loganx 思路分析 此题直接求解非常困难,可创设函数,再利用函数的图象求解不等式.由数列求和公式可知,原不等式可变形为 当n为奇数时,不等式①等价于logax>loga(x2-a);当n为偶数 y2=loga(x2-a),并作出它们的示意图(图26).由x2-a=x,解  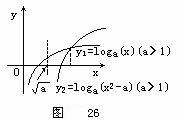 例28 四对夫妇出席一个晚会,见面时互相握手致意,巳知同一对夫妇互不握手,也没有一个人与另一个握2次手.之后,男甲问另外七人各握手几次,回答各不相同.问男甲的妻子握了几次手? 思路分析 这种非常规的数学问题,利用图形直观来解决也很有效.  用A、A′,B、B′,C、C′,D、D′表示四对夫妇,由回答握手次数各不相同可知,除男甲外的其余七人握手次数各为0,1,2,…,6次.不妨设A握了6次手,由图13-27可知此时B、B′、C、C′、D、D′已各握了一次手,所以A′只能握0次手;其次不妨设B握了5次手,由图13-28同理可知B′握了1次手;再次设C握了4次手,由图可知C′握了2次手;由于D、D′至少握了3次手,D、D′必有一人为3次,而另一人也不可能多于3次,否则改变其余人的握手次数,所以D与D′都握了3次手,即男甲与其妻子都是握了3次手. 形数结合是研究数学问题并实现问题的模型转换的一种基本思想和基本方法,它能沟通数与形的内在联系.在解题中学会以形论数、借数解形、数形结合,直观又入微,提高形数联想的灵活性,有助于思维素质的发展,有利于提高解题能力. (责任编辑:admin) |
