|
广东省中山市东升高中 高建彪 解三角形的知识本身是从人类长期的生产和生活实践中产生和发展起来的,在数学发展历史上,受到天文测量、航海测量和地理测量等方面实践活动的推动,解三角形的理论得到不断发展,并被用于解决许多测量问题. 下面我们来看看解三角形应用于一些测量方案的设计与研究. 一、怎样测量底部不可到达的建筑物的高度 问题:试设计一种方案,测量一山顶上的电视塔的顶部与地面的距离.  方案:选点C、D两次测得仰角 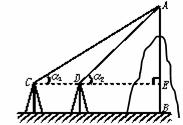 计算:(1)在△ACD中,利用正弦定理求出AD, (2)在Rt△ADE中,求出AE, 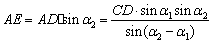 . .(3)AE+BE即为所求, 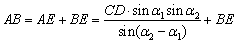 . .例题:如图,在某点 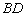 方向前进 方向前进 【解】在 根据正弦定理, 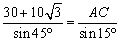 , ,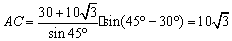 . .在 变式:如何测量山顶上的电视塔的高度呢?又如何测量河的宽度呢? 二、怎样在航行途中测出海上两个岛屿之间的距离 问题:如果你在海上直线航行,请设计一种测量海上两个小岛之间距离的方法. 方案:如图,A、B是已知的两个小岛,航船在时刻 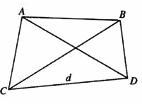 计算:(1)从C到D的距离 (2)在 (3)在 (4)在 例题:如图,在河对岸可以看到两个目标物 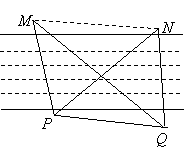 【解】在 根据正弦定理, 在 根据正弦定理, 在 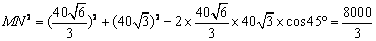 ∴ 两个目标物 变式:如何测量不能到达的两个点之间的距离. 三、怎样在水平飞行的飞机上测量飞机下方山顶的海拔高度 问题:飞机的航线和山顶在同一个铅直平面内,已知飞机的高度为海拔a,速度为v,如何在飞机上测量飞机下方山顶的海拔高度? 方案:飞机时刻 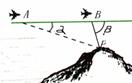 计算:(1)从A到B的距离 (2)在 (3)山顶海拔高度为 例题:飞机的航线和山顶在同一个铅直平面内,已知飞机的高度为海拔 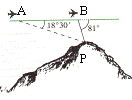 【解】 根据正弦定理, 解得 山顶的海拔高度为 变式:一辆汽车在一条水平的公路上向正东行驶,到A处时测得公路南侧远处一山顶D在东偏南15 的方向上,行驶5km后到达B处,测得此山顶在东偏南25 的方向上,仰角为8 ,求此山的高度CD. (答案:约1047米) 四、怎样测出海上航行的轮船的航速 问题:设计一种借助于两个观察点C、D(已知两个观察点之间的距离d)测量航船的速度的方案. 方案:船在时刻 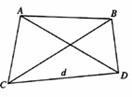 计算:(1)在 (2)在 (3)在 (4)计算速度 例题:已知两个观察点C、D之间的距离CD=80米,航船在A处时,测得 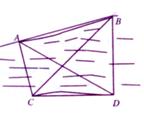 解】在 根据正弦定理, 在 ∴ 在 根据余弦定理, 所以,航船的速度 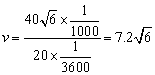 (千米/小时). (千米/小时).变式:可以探索与“测量不能到达的两个点之间的距离”的相同之处与不同之点.也可以研究如何测量航船的航向. 在以上方案的设计与研究中,我们可以看出,解三角形知识在实践中测量方面有着广泛的应用. 我们在今后的学习中需要加强动手实践,提高利用数学知识解决实际问题的能力,深刻认识数学在生产、生活实际中所发挥的作用. (责任编辑:admin) |
