《3.3 直线的交点坐标与距离公式(1)》测试题
一、选择题
1.(2009天津理改编)已知点A( )到直线 )到直线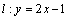 的距离为 的距离为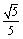 ,则点A的坐标为( ). ,则点A的坐标为( ).
A.(0,-2) B.(2,4) C.(0,-2)或(2,4) D.(1,1)
考查目的:考查点到直线的距离公式,以及分类讨论思想.
答案:C.
解析:直线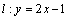 可化为 可化为 ,依题意得 ,依题意得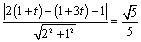 ,整理得 ,整理得 ,∴ ,∴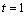 或 或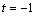 .当 .当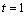 时,点A的坐标为(2,4);当 时,点A的坐标为(2,4);当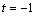 时,点A的坐标为(0,-2),故答案选C. 时,点A的坐标为(0,-2),故答案选C.
2.到直线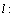 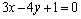 的距离为3,且与直线 的距离为3,且与直线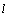 平行的直线 平行的直线 方程是( ). 方程是( ).
A. B. B. 或 或
C.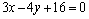 D. D.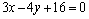 或 或
考查目的:考查相互平行的两条直线方程的特征,以及点到直线的距离公式.
答案:D.
解析:设直线 的方程为 的方程为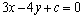 .在直线 .在直线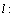 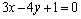 上任取一点P(1,1).∵ 上任取一点P(1,1).∵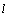 与 与 之间的距离为3,∴ 之间的距离为3,∴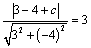 ,解得 ,解得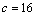 或 或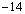 ,∴直线 ,∴直线 的方程为 的方程为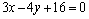 或 或 . .
3.若直线 : :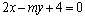 和直线 和直线 : : 的交点P位于第二象限,则 的交点P位于第二象限,则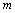 的取值范围是( ). 的取值范围是( ).
A.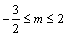 B. B. C. C.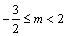 D. D.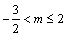
考查目的:考查两条直线的交点与二元一次方程组解的关系,一元一次不等式的解法及转化化归思想.
答案:B.
解析:解方程组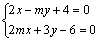 得直线 得直线 , , 的交点P的坐标为 的交点P的坐标为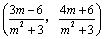 .∵点P位于第二象限,∴ .∵点P位于第二象限,∴ ,∵ ,∵ ,∴不等式组可化为 ,∴不等式组可化为 ,解得 ,解得 . .
二、填空题
4.若直线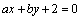 与直线 与直线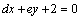 的交点为(3,-2),则经过点A( 的交点为(3,-2),则经过点A(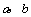 ),B( ),B(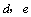 )的直线方程是 . )的直线方程是 .
考查目的:考查直线的方程,以及两条直线的交点与二元一次方程组的解的关系.
答案: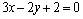 . .
解析:由题意得,点(3,-2)的坐标满足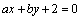 与 与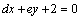 ,∴ ,∴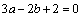 且 且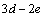
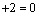 ,即点A( ,即点A(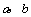 ),B( ),B(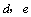 )的坐标都适合方程 )的坐标都适合方程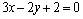 ,∴经过点A( ,∴经过点A(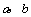 ),B( ),B(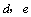 )的直线方程是 )的直线方程是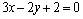 . .
5.已知点A(-3,8)、B(2,2),点P是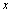 轴上的点,则当 轴上的点,则当 取最小值时,点P的坐标为 . 取最小值时,点P的坐标为 .
考查目的:考查两点之间线段最短、点关于直线对称的性质作图和直线方程的应用.
答案:(1,0).
解析:点A(-3,8)关于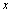 轴的对称点为 轴的对称点为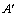 (-3,-8),根据对称性可得 (-3,-8),根据对称性可得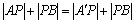 .当 .当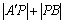 取得最小值时,点P是直线 取得最小值时,点P是直线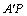 与 与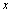 轴的交点.根据点 轴的交点.根据点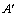 (-3,-8)、B(2,2)可求得,直线 (-3,-8)、B(2,2)可求得,直线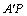 的方程为 的方程为 ,直线 ,直线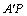 与 与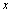 轴的交点P的坐标为(1,0). 轴的交点P的坐标为(1,0).
6.已知直线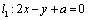 , ,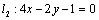 ,若直线 ,若直线 、 、 的距离等于 的距离等于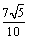 ,且直线 ,且直线 不经过第四象限,则 不经过第四象限,则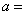 . .
考查目的:考查点到直线的距离公式,及两条直线平行关系的判断.
答案:3.
解析:由直线 、 、 的方程可知,直线 的方程可知,直线 ∥ ∥ .在直线 .在直线 上选取一点P(0, 上选取一点P(0,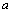 ),依题意得, ),依题意得, 与 与 的距离 的距离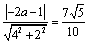 ,整理得 ,整理得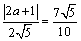 ,解得 ,解得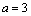 或 或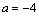 .∵直线 .∵直线 不经过第四象限,∴ 不经过第四象限,∴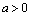 ,∴ ,∴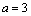 . .
三、解答题
7.(2011安徽文改编)设直线 : :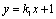 , , : : ,其中实数 ,其中实数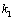 , ,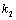 满足 满足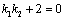 ,证明直线 ,证明直线 与 与 的交点在曲线 的交点在曲线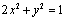 上. 上.
考查目的:考查两条直线的交点与二元一次方程组的解的关系,以及曲线与方程的关系.
解析:解方程组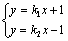 得 得 、 、 的交点P的坐标( 的交点P的坐标(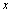 , ,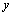 )为 )为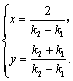
∵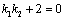 ,即 ,即 ,∴ ,∴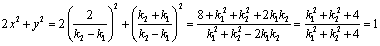 ,∴直线 ,∴直线 与 与 交点P( 交点P(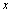 , ,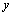 )在曲线 )在曲线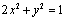 上. 上.
8.⑴求经过两条直线 : :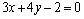 与 与 : :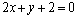 的交点 的交点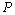 ,且垂直于直线 ,且垂直于直线 : :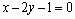 的直线 的直线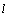 的方程; 的方程;
⑵已知直线 经过点 经过点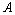 (0,1),直线 (0,1),直线 经过点 经过点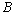 (5,0),且直线 (5,0),且直线 ∥ ∥ , ,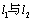 的距离为5,求直线 的距离为5,求直线 , , 的方程. 的方程.
考查目的:考查两直线的交点求法,平行线间的距离公式,两条直线垂直时的方程关系的应用,直线方程的求法.
答案:⑴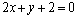 ;⑵ ;⑵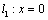 , ,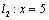 ,或 ,或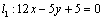 , ,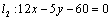 . .
解析:⑴解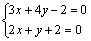 得 得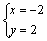 ,∴点P的坐标是(-2,2).∵ ,∴点P的坐标是(-2,2).∵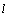 ⊥ ⊥ ,∴可设直线 ,∴可设直线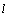 的方程为 的方程为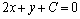 .把点P的坐标代入得 .把点P的坐标代入得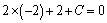 ,解得 ,解得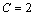 ,∴直线 ,∴直线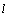 的方程为 的方程为 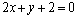 . .
⑵∵直线 ∥ ∥ ,∴当直线 ,∴当直线 , , 垂直于 垂直于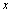 轴时,直线 轴时,直线 的方程为 的方程为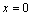 ,直线 ,直线 的方程为 的方程为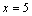 ,这时直线 ,这时直线 、 、 之间的距离等于5,符合题意;当直线 之间的距离等于5,符合题意;当直线 , , 不垂直于 不垂直于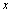 轴时,可设其斜率为 轴时,可设其斜率为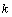 ,依题意得,直线 ,依题意得,直线 的方程为 的方程为 ,即 ,即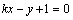 ,直线 ,直线 的方程为 的方程为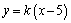 ,即 ,即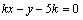 .在直线 .在直线 上取点 上取点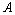 (0,1),∴点A到直线 (0,1),∴点A到直线 的距离 的距离 ,解得 ,解得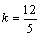 ,∴直线 ,∴直线 的方程为 的方程为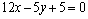 ,直线 ,直线 的方程为 的方程为 .综上得,符合题意的直线 .综上得,符合题意的直线 、 、 的方程有两组: 的方程有两组: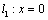 , ,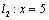 ,或 ,或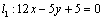 , ,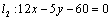 . .
(责任编辑:admin)
|
 ,∵
,∵