南昌市高中新课程训练题(三角函数2)
http://www.newdu.com 2025/07/12 03:07:07 人民教育出版社 佚名 参加讨论
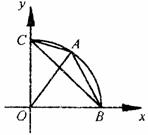
南昌市高中新课程训练题(三角函数2) 命题人:江西师大附中 戴翠红 一、选择题(本题共12小题,每小题5分,共60分). 1.设 A. 2.已知 A. 3.若函数 A. C. 4.已知 A. 5.已知 A.0 B.2 C. 6.已知等腰 A. 7.设 A. 8.设函数 A. 9.化简 A. 10. A.正三角形 B.等腰三角形 C.直角三角形 D.等腰直角三角形 11.函数 A. C.  12.将函数 A. 二、填空题(本题共4小题,每小题4分,共16分). 13.已知 14.已知 15.已知 16. 给出下列五个命题,其中正确命题的序号为 (1)函数 (2)函数 (3)函数 (4)函数 (5)函数 三、解答题(本题共6小题,共74分) 17. 求函数 18. 求函数 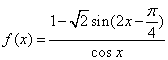 的定义域、最小正周期及单调增区间. 的定义域、最小正周期及单调增区间.19. 设函数 (1) 求   20. 在△ABC中,A(cosθ,sinθ)、B(1,0)、C(0,1)( (1)用θ表示△ABC的面积S(θ); (2)求△ABC面积的最大值; (3)函数y=S(θ)的图象可由函数y=sinθ的图象经过怎样变换得到. 21.求函数 22.已知A、B、C是 (1)证明: 参考答案 一、 选择题
二、填空题 13. 三、解答题 17.解: 当 18.解:由 故 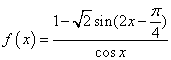  故最小正周期为 由 故单调增区间为 19.解:(Ⅰ) (Ⅱ)由(Ⅰ)知 由题意得 所以函数 (Ⅲ)由
 20.解: ∴A、B、C三点都在单位圆上,且A点在第一象限, 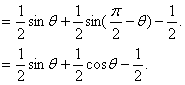 =
 (2) (3)函数 21.解: 注意到 即 22.(1)证明: (2) 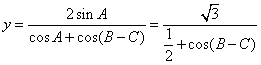 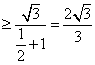 当且仅当B=C=600时 (责任编辑:admin) |