《3.3 直线的交点坐标与距离公式(2)》测试题
一、选择题
1.已知点O为原点,点P在直线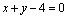 上,则 上,则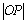 的最小值是( ). 的最小值是( ).
A.2 B.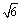 C. C.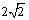 D. D.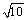
考查目的:考查点到直线的垂线段最短的应用,以及点到直线的距离公式.
答案:C.
解析:由题意得,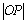 的最小值就是原点到直线 的最小值就是原点到直线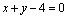 的距离.由点到直线的距离公式得, 的距离.由点到直线的距离公式得,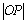 的最小值为 的最小值为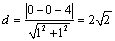 . .
2.(2011北京文)已知点A(0,2),B(2,0).若点C在函数 的图象上,则使得 的图象上,则使得 的面积为2的点C的个数为( ). 的面积为2的点C的个数为( ).
A.4 B.3 C.2 D.1
考查目的:考查点到距离公式的应用和数形结合的思想方法.
答案:A.
解析:直线AB的方程为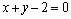 , ,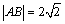 .设点C的坐标为( .设点C的坐标为( , ,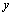 ),则点C到直线AB的距离 ),则点C到直线AB的距离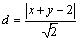 .∵点C在曲线 .∵点C在曲线 上,∴ 上,∴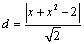 ,∴ ,∴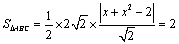 ,解得 ,解得 ,∴满足条件的点C有4个. ,∴满足条件的点C有4个.
3.点M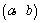 与N 与N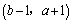 关于下列哪种图形对称?( ). 关于下列哪种图形对称?( ).
A.直线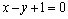 B.直线 B.直线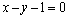 C.点( C.点( ) D.直线 ) D.直线
考查目的:考查中点坐标公式,以及点与直线对称的有关性质.
答案:A.
解析:线段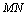 的中点K的坐标为 的中点K的坐标为 ,经验证可得,点K的坐标适合方程 ,经验证可得,点K的坐标适合方程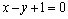 ,故答案选A. ,故答案选A.
二、填空题
4.若点O(0,0),A(4,-1)到直线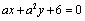 的距离相等,则实数 的距离相等,则实数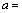 ________. ________.
考查目的:考查点到直线的距离公式.
答案:-2或4或6.
解析:由题意得 ,即 ,即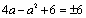 ,解得 ,解得 ,或 ,或 ,或 ,或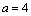 ,或 ,或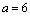 .经检验得, .经检验得, 不合题意,舍去,∴ 不合题意,舍去,∴ ,或 ,或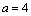 ,或 ,或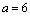 . .
5.若 为任意实数,则直线 为任意实数,则直线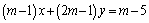 一定经过定点 . 一定经过定点 .
考查目的:考查直线与直线的位置关系的应用.
答案:(9,-4).
解析:将直线方程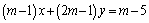 整理为 整理为 ①.∵ ①.∵ 为任意实数,∴要使①成立,必须 为任意实数,∴要使①成立,必须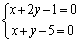 ,解得 ,解得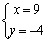 ,即直线 ,即直线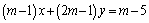 一定经过点(9,-4).本题也可根据 一定经过点(9,-4).本题也可根据 为任意实数,令 为任意实数,令 和 和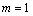 得到两个关于 得到两个关于 , ,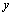 的方程,通过解方程组得出交点的坐标. 的方程,通过解方程组得出交点的坐标.
6.(2009全国Ⅰ文)若直线 被两条平行线 被两条平行线 : : 与 与 : : 截得的线段长为 截得的线段长为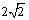 ,则直线 ,则直线 的倾斜角可以是:① 的倾斜角可以是:①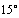 ;② ;②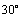 ;③ ;③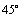 ;④ ;④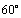 ;⑤ ;⑤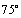 ,其中正确答案的序号是 .(写出所有正确答案的序号) ,其中正确答案的序号是 .(写出所有正确答案的序号)
考查目的:考查点到直线的距离公式,直线倾斜角与斜率的概念,以及分类讨论思想.
答案:①⑤.
解析:易求两条平行线 , , 之间的距离为 之间的距离为 .画示意图可知,要使直线 .画示意图可知,要使直线 被两条平行线 被两条平行线 , , 截得的线段长为 截得的线段长为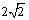 ,必须使直线 ,必须使直线 与直线 与直线 , , 成 成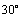 的夹角.∵直线 的夹角.∵直线 , , 的倾斜角为 的倾斜角为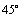 ,∴直线 ,∴直线 的倾斜角等于 的倾斜角等于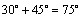 或 或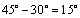 . .
三、解答题
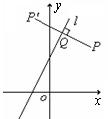
7.⑴已知直线 : :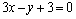 ,求点P(4,5)关于直线 ,求点P(4,5)关于直线 的对称点; 的对称点;
⑵已知直线 : :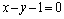 , , : :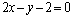 .若直线 .若直线 与 与 关于直线 关于直线 对称,求直线 对称,求直线 的方程. 的方程.
考查目的:考查点关于直线的对称点的求法,两条直线关于某一条直线对称的点的性质,以及数形结合思想等.
答案:⑴(-2,7);⑵ . .
解析:⑴设点P关于直线 的对称点为 的对称点为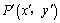 . .
∵ ,直线 ,直线 的斜率为3,∴ 的斜率为3,∴ , ,
∴直线 的方程为 的方程为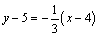 ,即 ,即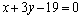 . .
设 交直线 交直线 于点Q,∴解 于点Q,∴解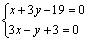 得 得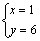 ,即点Q的坐标是(1,6). ,即点Q的坐标是(1,6).
∵Q是线段 的中点,∴ 的中点,∴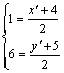 ,解得 ,解得 , ,
∴点P关于直线 的对称点 的对称点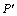 的坐标为(-2,7). 的坐标为(-2,7).
⑵∵直线 与 与 关于直线 关于直线 对称,∴ 对称,∴ 上任意一点关于 上任意一点关于 的对称点都在 的对称点都在 上, 上,
∴直线 与 与 的交点A(1,0)在直线 的交点A(1,0)在直线 上. 上.
易知点(0,-2)为直线 上一点,设其关于直线 上一点,设其关于直线 的对称点为B( 的对称点为B( , ,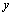 ), ),
则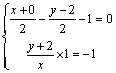 ,解得 ,解得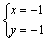 ,∴点A(1,0)、B(-1,-1)均为 ,∴点A(1,0)、B(-1,-1)均为 上两点. 上两点.
由点A、B的坐标可求得,直线 的方程为 的方程为 . .
8.直线 被两条直线 被两条直线 : :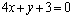 和 和 : :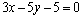 截得的线段的中点为P(-1,2),求直线 截得的线段的中点为P(-1,2),求直线 的方程. 的方程.
考查目的:考查中点坐标公式,两条直线的交点与方程组的解的关系,数形结合思想等.
答案: . .
解析:(方法一)设直线 与 与 的交点为A( 的交点为A(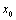 , ,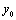 ).由已知条件得,直线 ).由已知条件得,直线 与 与 的交点为B( 的交点为B(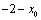 , ,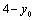 ),且满足 ),且满足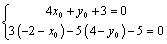 ,即 ,即 ,解得 ,解得 ,∴直线 ,∴直线 的方程为 的方程为 ,即 ,即 . .
(方法二)若直线 的斜率不存在,则其方程为 的斜率不存在,则其方程为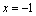 .直线 .直线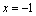 与直线 与直线 , , 的交点分别为A(-1,1),B(-1, 的交点分别为A(-1,1),B(-1,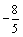 ),显然线段AB的中点不是点P,不符合题意,∴直线 ),显然线段AB的中点不是点P,不符合题意,∴直线 的斜率存在.设直线 的斜率存在.设直线 的方程为 的方程为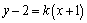 ,整理得 ,整理得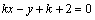 .解 .解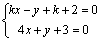 得 得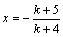 ;解 ;解 得 得 ,∴ ,∴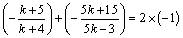 ,解得 ,解得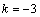 ,∴直线 ,∴直线 的方程为 的方程为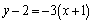 ,即 ,即 . .
(责任编辑:admin)
|

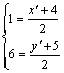 ,解得
,解得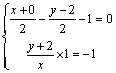 ,解得
,解得