|
下面是高中数学老师总结的高中数学简单的逻辑联结词、全称量词与存在量词知识点梳理及高频考点剖析,助力高三理科生高效备战一轮复习!  【核心素养分析】 1.了解逻辑联结词“或”“且”“非”的含义。 2.理解全称量词和存在量词的意义。 3.能正确地对含一个量词的命题进行否定。 4.重点培养逻辑推理的学科素养。 【知识梳理】 1.简单的逻辑联结词 (1)命题中的且、或、非叫做逻辑联结词. (2)命题p且q、p或q、非p的真假判断 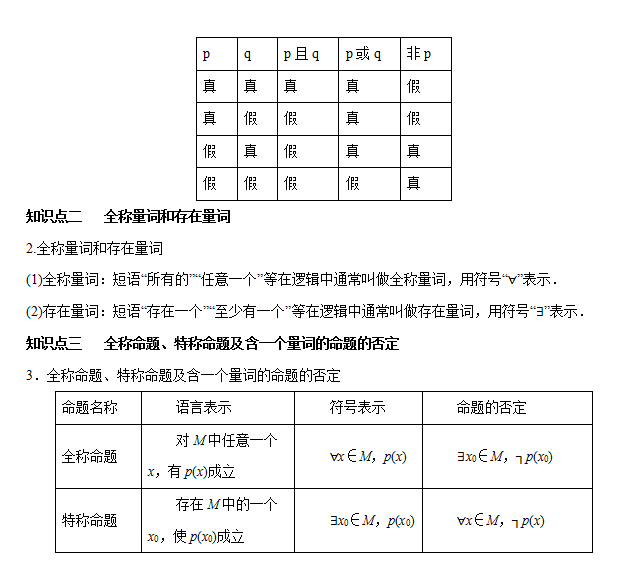 【典例剖析】 高频考点一 含有逻辑联结词的命题的真假判断 例1、 (2020·山西平遥中学模拟) 设a,b,c是非零向量.已知命题p: 若a·b=0,b·c=0,则a·c=0;命题q:若a∥b,b∥c,则a∥c.则下列命题中真命题是( ) A.p∨q B.p∧q C.(┐p)∧(┐q) D.p∧(┐q) 【答案】B 【解析】取a=c=(1,0),b=(0,1),显然a·b=0,b·c=0,但a·c=1≠0,∴p是假命题. 又a,b,c是非零向量, 由a∥b知a=xb(x∈R),由b∥c知b=yc(y∈R), ∴a=xyc,∴a∥c,∴q是真命题. 综上知p∨q是真命题,p∧q是假命题. ┐p为真命题,┐q为假命题. ∴(┐p)∧(┐q),p∧(┐q)都是假命题. 【规律方法】 1.“p∨q”、“p∧q”、“┐p”形式命题真假的判断关键是对逻辑联结词“或”“且”“非”含义的理解,其操作步骤是:(1)明确其构成形式;(2)判断其中命题p,q的真假;(3)确定“p∨q”“p∧q”“┐p”形式命题的真假. 2.p∧q形式是“一假必假,全真才真”,p∨q形式是“一真必真,全假才假”,┐p则是“与p的真假相反”. 【变式探究】 (2020·吉林长春市实验中学模拟) 已知命题p:?x∈R,x2-x+1≥0;命题q:若a2<b2,则a<b.下列命题为真命题的是( ) A.p∧q B.p∧┐q C.┐p∧q D.┐p∧┐q 【答案】B 【解析】∵一元二次方程x2-x+1=0的判别式Δ=(-1)2-4×1×1<0,∴x2-x+1>0恒成立, ∴p是真命题,┐p为假命题. ∵当a=-1,b=-2时,(-1)2<(-2)2,但-1>-2, ∴q为假命题,┐q为真命题. ∴p∧┐q为真命题,p∧q,┐p∧q,┐p∧┐q为假命题. 高频考点二 全称(特称)命题的真假判断 例2、 (2020·浙江效实中学模拟) 已知定义域为R的函数f(x)不是偶函数,则下列命题一定为真命题的是( ) A.x∈R,f(-x)≠f(x) B.x∈R,f(-x)≠-f(x) C.x0∈R,f(-x0)≠f(x0) D.x0∈R,f(-x0)≠-f(x0) 【答案】C 【解析】∵定义域为R的函数f(x)不是偶函数,∴x∈R,f(-x)=f(x)为假命题,∴x0∈R,f(-x0)≠f(x0)为真命题. 【规律方法】 1.全称命题与特称命题的否定与命题的否定有一定的区别,否定全称命题和特称命题时,一是要改写量词,全称量词改写为存在量词,存在量词改写为全称量词;二是要否定结论,而一般命题的否定只需直接否定结论. 2.判定全称命题“∈M,p(x)”是真命题,需要对集合M中的每一个元素x,证明p(x)成立;要判断特称命题是真命题,只要在限定集合内至少找到一个x=x0,使p(x0)成立.   (责任编辑:admin) |
