|
很多高中学生都感觉学习数学很吃力,但是函数却是高考重要考点,下面小编整理了函数的单调性与最值的考点归纳,供2020年高考生参考,备战一轮复习,提高学习效率。  一、基础知识 1.增函数、减函数 定义:设函数f(x)的定义域为I: (1)增函数:如果对于定义域I内某个区间D上的任意两个自变量的值x1,x2,当x1<x2时,都有f(x1)<f(x2),那么就说函数f(x)在区间D上是增函数. (2)减函数:如果对于定义域I内某个区间D上的任意两个自变量的值x1,x2,当x1<x2时,都有f(x1)>f(x2),那么就说函数f(x)在区间D上是减函数. 增(减)函数定义中的x1,x2的三个特征 一是任意性;二是有大小,即x1<x2(x1>x2);三是同属于一个单调区间,三者缺一不可. 2.单调性、单调区间 若函数y=f(x)在区间D上是增函数或减函数,则称函数y=f(x)在这一区间具有(严格的)单调性,区间D叫做函数y=f(x)的单调区间. 有关单调区间的两个防范 (1)单调区间只能用区间表示,不能用不等式表示. (2)有多个单调区间应分别写,不能用符号“∪”连接,也不能用“或”连接,只能用“逗号”或“和”连接. 3.函数的最值 设函数y=f(x)的定义域为I,如果存在实数M满足: (1)对于任意的x∈I,都有f(x)≤M或f(x)≥M. (2)存在x0∈I,使得f(x0)=M. 那么,我们称M是函数y=f(x)的最大值或最小值. 函数最值存在的两条结论 (1)闭区间上的连续函数一定存在最大值和最小值.当函数在闭区间上单调时最值一定在端点取到. (2)开区间上的“单峰”函数一定存在最大(小)值. 二、常用结论 在公共定义域内: (1)函数f(x)单调递增,g(x)单调递增,则f(x)+g(x)是增函数; (2)函数f(x)单调递减,g(x)单调递减,则f(x)+g(x)是减函数; (3)函数f(x)单调递增,g(x)单调递减,则f(x)-g(x)是增函数; (4)函数f(x)单调递减,g(x)单调递增,则f(x)-g(x)是减函数; (5)若k>0,则kf(x)与f(x)单调性相同;若k<0,则kf(x)与f(x)单调性相反; (6)函数y=f(x)(f(x)>0)在公共定义域内与y=-f(x),y=的单调性相反; (7)复合函数y=f[g(x)]的单调性与y=f(u)和u=g(x)的单调性有关.简记:“同增异减”. 考点一 确定函数的单调性?区间?) [典例] (1)求函数f(x)=-x2+2|x|+1的单调区间. (2)试讨论函数f(x)=(a≠0)在(-1,1)上的单调性.  [解题技法] 判断函数单调性和求单调区间的方法 (1)定义法:一般步骤为设元―→作差―→变形―→判断符号―→得出结论. (2)图象法:如果f(x)是以图象形式给出的,或者f(x)的图象易作出,则可由图象的上升或下降确定单调性. (3)导数法:先求导数,利用导数值的正负确定函数的单调性及区间. (4)性质法:对于由基本初等函数的和、差构成的函数,根据各初等函数的增减性及复合函数单调性性质进行判断;复合函数单调性,可用同增异减来确定. [题组训练]  考点二 求函数的值域最值 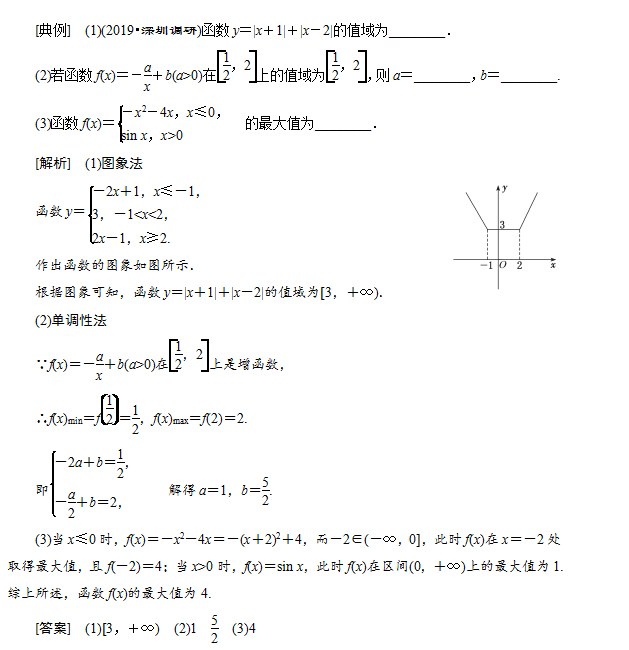 [提醒] (1)求函数的最值时,应先确定函数的定义域. (2)求分段函数的最值时,应先求出每一段上的最值,再选取其中最大的作为分段函数的最大值,最小的作为分段函数的最小值. [题组训练]   考点三 函数单调性的应用 考法(一) 比较函数值的大小 [典例] 设偶函数f(x)的定义域为R,当x∈[0,+∞)时,f(x)是增函数,则f(-2),f(π),f(-3)的大小关系是( ) A.f(π)>f(-3)>f(-2) B.f(π)>f(-2)>f(-3) C.f(π)<f(-3)<f(-2) D.f(π)<f(-2)<f(-3) [解析] 因为f(x)是偶函数,所以f(-3)=f(3),f(-2)=f(2). 又因为函数f(x)在[0,+∞)上是增函数. 所以f(π)>f(3)>f(2),即f(π)>f(-3)>f(-2). [答案] A [解题技法] 比较函数值大小的解题思路 比较函数值的大小时,若自变量的值不在同一个单调区间内,要利用其函数性质,转化到同一个单调区间内进行比较,对于选择题、填空题能数形结合的尽量用图象法求解.  [解题技法] 求解含“f”的函数不等式的解题思路 先利用函数的相关性质将不等式转化为f(g(x))>f(h(x))的形式,再根据函数的单调性去掉“f”,得到一般的不等式g(x)>h(x)(或g(x)<h(x)).  [解题技法] 利用单调性求参数的范围(或值)的方法 (1)视参数为已知数,依据函数的图象或单调性定义,确定函数的单调区间,与已知单调区间比较求参数; (2)需注意若函数在区间[a,b]上是单调的,则该函数在此区间的任意子集上也是单调的. [题组训练]  (责任编辑:admin) |
