|
利用能量法计算物体作简谐运动的周期 浙江省桐乡市高级中学 胡亦中 当物体作简谐运动时，求振动周期的常用方法是利用动力学方法，即利用回复力F＝-kx，由周期  求得。但当系统受力较难分析时，可利用能量法求解。下面以弹簧振子为例进行分析：1．基本规律 以水平方向弹簧振子为例，设振子的位移x随时间的变化规律为x＝Acos（wt+  ），在振动中的任何一时刻t时，振子具有动能EK，弹簧具有弹性势能EP。此两者的值分别为 ， 。由于k＝mw2，故上式又可写为  。可见这一振动系统的动能和势能都随时间作周期性变化，但系统总的机械能E＝EK+EP＝  保持不变。这一总机械能与振幅的平方成正比，与角频率的平方成正比。这也是简谐运动的一般规律。简谐运动能量的表达式还为我们提供了求振子频率的另一种方法，这种方法不涉及振子所受的力，因此在力不易求得时较为方便。若将势能EP写成位移x的函数，由前述势能的表达式可得到 w＝  ，或将总能量写成振幅的函数，则由前述总能量的表达式可以得到 w＝  。2．用能量法求周期的规律应用 【例1】有一轻质刚性杆，长为L，可绕上端的水平轴自由转动，下端固定着质量为m的质点，构成单摆。如图1所示，质点通过一根劲度系数为k的水平弹簧拴到墙上，当摆竖直下垂时，弹簧处于松弛状态，求系统小幅度振动的周期。  解析：设质点偏离平衡位置的最大位移为x，杆偏离竖直方向的夹角为θ，则系统总的机械能为  ，式中x＝Lθ， 1-cosθ＝  。故得  ，而  ，比较上两式得系统的角频率为  ，故系统振动的周期为  。【例2】如图2所示，摆球质量为m，凹形滑块质量为M，摆长为l。m与M、M与水平面之间光滑，令摆线偏转很小角度后，从静止释放，求系统的振动周期。  解析：设未放凹形滑块的单摆以角频率w振动，偏角为θ，振幅A＝lθ。由系统振动能量守恒得 mgl（1-cosθ）＝  ，设带有凹形滑块的摆以同样的振幅以角频率为w′振动，则有 mgl（1-cosθ）＝  ，由上两式得  ，而 故系统的振动周期为  。通过以上两例可知采用能量法求周期的一般步骤： （1）确定振动系统，分析振动系统的机械能是否守恒； （2）找出平衡位置并将选定为坐标原点； （3）写出任意位置处的机械能表达式（或特殊位置）； （4）将求得的结果与弹簧作简谐运动时能量关系作比较，求得系统振动周期。 3．巩固练习 【例1】如图3所示，质量为m的小球用轻杆悬挂，两侧用劲度系数为k的弹簧连接，杆自由下垂，弹簧无形变，图中已知，求摆杆作简谐运动的周期。 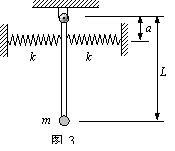 （答案：  ）【例2】一个单摆，由一根刚性轻杆和杆端质量为m的重物组成，做微小振幅的自由振动。如果在杆上某点再固定一个和杆端重物质量相同的重物，使原单摆变成一个异形复摆，其振动周期最多改变百分之几？ （答案：9%） (责任编辑：admin) |