|
Excel软件研究虹的散色角 江西省南丰一中 聂应才 摘要:虹是我们生活中常见的自然现象,其五颜六色为之感叹。颜色的排布为什么红色在最上面、紫色在最下面,这就涉及到虹的散色角问题,许多资料直接告诉了结果[1],就是有计算过程,也用了电脑编程模拟[2]或笛卡儿的求导思想[3],都是中学学生难以接受、理解的方法。本文利用Excel软件,轻松地解决了过程的复杂性,学生能够自主研究出虹的散色角。 关键词:Excel 散色角 2002广东物理高考试题第17题为:雨过天晴,人们常看到天空中出现彩虹,它是由阳光照射到空中弥漫的水珠上时出现的现象。在说明这个现象时,需要分析光线射入水珠后的光路。一细束光线射入水珠,水珠可视为一个半径为R的球,球心O到入射光线的垂直距离为d,水的折射率为n。 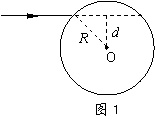 (1)在图1上画出该束光线射入水珠内经一次反射后又从水珠中射出的光路图。 (2)求这束光线从射向水珠到射出水珠每一次偏转的角度。  由于彩虹在现行高中教材中没有出现,所以题目中介绍了虹的一些背景知识:是光经两次折射、一次反射的结果。为了简化,此题没有涉及入射光是复合光──白光,而实际上是白光,这样就有色散问题,也就空中出现彩色,如图2所示,从图中观察到颜色分布从上而下是红、橙、黄、绿、蓝、靛、紫。其分布规律就是求虹的散色角。 1.虹的散色角 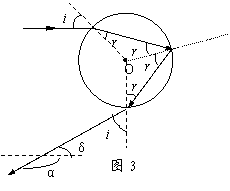 图3为光线进入水滴后反射与折射的情形,光线射出方向与入射方向的夹角称为偏向角α,而地上观察者观测的角度称为散色角δ,由图知 α+δ=180°, ① 由图中几何,可得到 δ=4r-2i ② 式中i为入射角,r为折射角,设水的折射率为n,由折射定律有 所以散色角δ 2.Excel软件处理及结果 入射角i从0到90°,每0.1°由公式④可计算一次散色角δ,以虹的红色光(n=1.3311)为例说明在Excel软件中如何处理。 (1)启动Excel软件,在A1单元格中输入0,A2单元格中输入0.1,把A1和A2单元格都选中,然后往下拖动,一直到A901单元格为止,这样得到从0到90°、每次增加0.1°的901个入射角角度数据。 (2)选中B1单元格,在编辑栏中输入“=4*ASIN(SIN(A1*PI()/180)/1.3311)*180/PI()-2*A1”,如图4所示。需要说明的是:在A1~A901单元格中输入的数据是角度制,而Excel软件中三角函数是弧度制,因此有角度制和弧度制之间的换算问题。
 (3)选中B1单元格,往下拖,一直拖到B901单元格,这样就得到入射角i的相应散色角δ。当选中B85时,其编辑栏中A1就变成相应的A85。
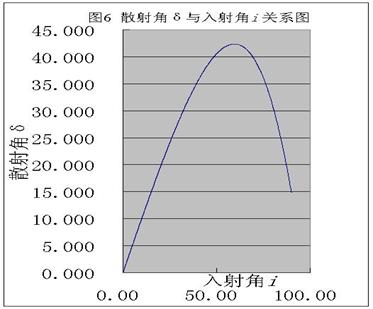
 (4)同时选中A和B,把A和B栏中数据都选中,利用Excel软件的图表向导功能,图表类型中为“xy散点图”中“无数据点平滑线散点图”,如图5所示。形成散色角δ与入射角i关系图,如图6所示。
 图6 笛卡儿的虹霓理论:他认为不同的入射角对应不同的偏向角中,只有最小偏向角才是我们观测到的虹霓的方向。由公式①可知,偏向角最小时,散色角就最大,即图6所示曲线中的最高点,从B单元格中,可知最大值为42.355°。对于紫光单色光,其折射率为1.3435,处理时,只需要将B单元格中编辑栏中1.3311改为1.3435,那么图6中的曲线和B单元格的数据就会作出相应的变化,可知散色的最大角为40.575°。当然其他色光也作同样的处理,得到其他色光的散色角。所以虹的红色光在最上面,紫色光在最下面。 既然不同的入射角有不同的散色角,那为什么就看最大的散色角呢?让我们来分析一下入射角每增加1°时,其散色角变化是多少,由A单元和B单元的数据,很容易得到,如表所示。
入射角每增加1时,散色角变化相应的值 既然在入射角为59.1°~60.1°的范围间,射出光线最为集中,远比其他方向入射时,射出的光线要集中多多了,取入射角为59.5°,由B栏对应单元格的数据即为散色角,为δ=42.355°,而这与实际观测的仰角一致。当然其他色光如紫光也可以进行表的数值计算,可以得到射出光线最为集中的入射角,从而求出散色角。 参考文献: [1]王建忠.启东中学奥赛训练教程(高中物理).南京:南京师范大学出版社,2005.576. [2]廖向东.球形水珠色散的计算机模拟.教学仪器与实验,2005,9(4):23~24. [3]张仁昌.虹霓现象.http://www.phy.ntnu.edu.tw/demolab/index.htm (责任编辑:admin) |