|
平衡中的“死”与“活” 江西省萍乡市上栗中学 彭俊昌 一、“活结”与“死结” 绳是物体间连接的一种方式，当多个物体用绳连接的时候，其间必然有“结”的出现，根据“结”的形式不同，可以分为“活结”和“死结”两种。“活结”是绳子间的一种光滑连接，其特点是结的两端同一绳上的张力相等；而“死结”是绳子间的一种固定连接，结的两端绳子上的张力不一定相等。 例1．建筑工人要将建筑材料运送到高处，常在楼顶装置一个定滑轮（图-1中未画出），用绳AB通过滑轮将建筑材料提到某一高处，为了防止材料与墙壁相碰，站在地面上的工人还另外用绳CD拉住材料，使它与竖直墙面保持一定的距离L。若不计两根绳的重力，在提起材料的过程中，绳AB和CD的拉力T1和T2的大小变化情况是（ ） A．T1增大、T2增大 B．T1增大、T2不变 C．T1增大、T2减小 D．T1减小、T2减小  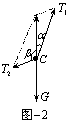 解析：三根绳子连接于C点不动，所以属于“死结”的问题，三根绳上的张力不相等，画出C点的受力如图-2所示，因材料在上升过程中与墙保持L的距离不变，所以上升过程中α和β均增大，由力的平行四边形定则可知，T1、T2均增大，所以正确答案为A。 例2．如图-3所示，相距4m的两根固定柱子拴上一根长5m的细绳，小滑轮及绳子的质量，摩擦均不计。当滑轮上吊一重180N的重物时，求绳子中的张力？   解析：因滑轮可以在绳上自由滑动，所以滑轮与绳接触的点为“活结”，跨过滑轮的两段绳子上的张力相等，画出其受力如图-4所示。由几何关系知：  ，所以α=53?，绳中的张力F= N=150N。二、“活杆”与“死杆” 轻杆是物体间连接的另一种方式，根据轻杆与墙壁连接方式的不同，可以分为“活杆”与“死杆”。所谓“活杆”，就是用铰链将轻杆与墙壁连接，其特点是杆上的弹力方向一定沿着杆的方向；而“死杆”就是将轻杆固定在墙壁上（不能转动），此时轻杆上的弹力方向不一定沿着杆的方向。 例3．如图-5所示，绳与杆均轻质，承受弹力的最大值一定，A端用铰链固定，滑轮在A点正上方（滑轮大小及摩擦均可不计），B端吊一重物。现施拉力F将B缓慢上拉（均未断），在AB杆达到竖直前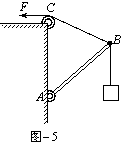（ ）   A．绳子越来越容易断 B．绳子越来越不容易断 C．AB杆越来越容易断 D．AB杆越来越不容易断 解析：因为轻杆AB是用铰链固定在墙壁上，所以AB是一根“活杆”，可知杆中的弹力方向一定沿着AB方向，而B点是一个“死结”，所以两根绳中的弹力不相等。画出B点的受力如图-6所示，由于力的矢量三角形与几何三角形ABC相似，所以有：  ，而在动态变化过程中，AB、AC、G不变，BC逐渐减小，所以得到FA不变，F逐渐减小。正确选项为B。例4．如图所示，硬杆BC的一端固定在墙上的B点，另一端装有滑轮C，重物D用绳拴住通过定滑轮固定于墙上的A点，若杆、滑轮及绳的质量和摩擦均不计，将绳的固定端从A点稍向下移，则在移动过程中（ ） A．绳的拉力、滑轮对绳的作用力增大 B．绳的拉力减小，滑轮对绳的作用力增大 C．绳的拉力不变，滑轮对绳的作用力增大 D．绳的拉力、滑轮对绳的作用力都不变  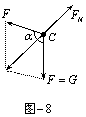 解析：因为轻杆BC固定在墙壁上，所以BC为“死杆”，而C端装有滑轮，所以C端相当于一个“活结”，滑轮两边绳上的弹力相等，均为F=G，画出C点的受力如图-8所示。当A点向下移动时，夹角α逐渐减小，而绳上的张力F不变，故FN增大，而FN的方向也发生变化，不沿杆的方向。正确选项为C。 通过上面的分析可以看出，我们在学习物理知识的时候，如果能将一些常见问题进行归类，抽象出一定的物理模型，有利于对所学知识的举一反三、触类旁通。 针对训练 1．如图所示，两个质量分别为m和4m的质点A、B之间用一轻杆固定，并用长为L的累绳挂在光滑的定滑轮上，求系统平衡时，OA、OB段绳各为多长？  （答案：AO=0．8L，BO=0．2L） 2．如图所示，轻杆AB和BC组成一个固定的三角形支架，重力不计的滑轮用轻绳OB系在B点，跨过滑轮的轻绳一端系一重物G=100N，另一端在拉力T的作用下匀速上升，求两根轻杆所受的作用力？   （答案：FA=946N，FB=669N） (责任编辑：admin) |