|
曲线运动题型与方法 陕西省宝鸡市陈仓区教研局教研室 邢彦君 一、曲线运动的特征与条件 曲线运动中，至少质点运动的速度方向是变化的。因此，曲线运动是变速运动，可以是匀变速曲线运动，也可以是非匀变速曲线运动。不管是那种曲线运动，共同的特征是加速度方向与速度方向不在同一条直线上，运动中速度的方向随时间在变化。若运动中加速度的大小、方向保持不变，属于匀变速曲线运动，如平抛运动。曲线运动的特征，还可以从力与运动的关系叙述，就是质点所受合外力的方向与速度方向不在同一条直线上。因此，质点做曲线运动的条件就是：运动质点所受外力的合力方向与速度方向不在一条直线上。曲线运动中，质点的速度方向总是朝合外力方向一侧偏转。若合外力恒定不变，质点是匀变速曲线运动。 例1．一质点在两个恒力的作用下做匀速直线运动，某时刻将其中一个力撤去，则质点将如何运动？ 解析：质点在两个恒力的作用下做匀速直线运动，由牛顿第一或第二定律知，这两个力必大小相等，方向相反。但这两个力的方向与质点运动的速度方向间是什么关系，题中未明确告诉，因此要分几种情况进行分析。 （1）若两力的方向与运动方向在一条直线上，必是一力与运动方向一致，另一力相反，若撤掉的是与运动方向一致的力，质点将做匀减速直线运动；若撤掉的是与运动方向相反的力，质点将做匀加速直线运动。 （2）若两力的方向与质点运动方向不在一条直线上，撤掉任一力后，由于剩下的一个恒力的方向与质点运动方向不在一条直线，质点将做匀变速曲线运动。 点评：曲线运动的条件是合力方向与速度方向不在一条直线。 二、运动的合成与分解 运动的合成与分解有两方面的应用。一是质点同时参与两个运动，比如小船渡河时，一面相对水面航行，一面随水漂流。这样，小船同时参与了两个运动，为了研究方便，可求出两个运动的合速度、合加速度——合运动，用合运动一个运动等效替代两个分运动，简化研究过程。另一方面的运用是将一个复杂的运动分解为同时进行着的两个较简单的运动，用同时进行着的两个运动等效替代一个复杂的运动。比如将曲线运动分解为两个直线运动，分别研究，求出两个分运动的速度、位移，然后运用平行四边形定则求出合速度与合位移，就是合运动的速度与位移。运动的合成与分解，关键是分清楚哪个是和运动，那些时分运动。 例2．两个相互垂直的匀变速直线运动的合运动是直线运动吗？ 解析：两个直线运动的合运动是直线运动还是曲线运动，就看合速度的方向是否随时间变化。若合速度方向不随时间变化，是直线运动，否则是曲线运动。设两个分运动的初速度分别为vo1、vo2，加速度分别为a1、a2。则t时刻两分运动的速度分别为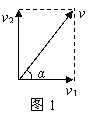：  ， 。运用平行四边形定则，此刻的合速度如图1中的对角线v所示，设它与v1方向的夹角为α，则有： 。由此式可以看出： （1）当vo1、vo2均等于零时，  与时间无关，即合速度方向不随时间变化，合运动为直线运动。（2）当a1、a2均等于零时，  与时间无关，即合速度的方向不随时间变化，合运动为直线运动（3）当两个分运动都是初速度不为零的匀加速直线运动或匀减速直线运动，且两个分运动的初速度与加速度数值相等，及两个分运动完全相同，表达式 中，分子分母相等， =1，速度方向不随时间变化，合运动是直线运动。除这三种情况外，合运动是曲线运动。 点评：曲线运动最基本的特点是速度方向随时间变化。 例3．如图2所示，A、B两车通过细绳跨接在定滑轮两侧，并分别置于光滑水平面上，若A车以速度v0向右匀速运动，当绳与水平面的夹角分别为α和β时，B车的速度是多少？  解析：A、B两车（质点、）沿水平面的运动（实际进行的运动）是合运动，根据实际效果，A的运动一方面时右边的绳变长，小车与绳的连接点具有沿绳斜向下的运动；一方面右边绳子与竖直方向的夹角增大，小车与绳的连接点有随绳绕滑轮向右转动的运动，具有垂直于绳斜向上的运动。因此，绳子速度vA可分解为垂直于绳斜向上的速度vA1和绳斜向下的速度vA2，如图3-a所示；同理，B的运动速度vB可分解为沿绳斜向上的速度vB1和垂直于绳斜向下的速度vB2，如图3-b所示。则：vA2=vocosβ，vB1=vBcosα。运动中绳不伸缩、不断裂，故有vA2＝vB1，解得B车的运动速度为：vB=vocosα/cosβ。 点评：运动的分解，关键是分清合运动与分运动，实际进行着的运动是合运动。 三、平抛运动问题 对于平抛运动问题的分析与求解，常涉及到高度、水平位移、速度、位移等。通常的处理方法是将平抛运动分解为水平方向的匀速直线运动和竖直方向的自由落体运动，但有时也可根据实际问题的特点及解题的需要，分解为其他方向的两个直线运动。 例4．如图4所示，从同一点O先后水平弹出的三个物体分别落在对面台阶上的A、B、C三点，若不计空气阻力，三物体平抛的初速度vA、vB、vC的关系以及三物体在空中的飞行时间tA、tB、tC的关系分别是   A．vA＞vB＞vC ，tA＞tB＞tC B．vA＜vB＜vC ，tA=tB=tC C．vA＜vB＜vC ，tA＞tB＞tC D．vA＞vB＞vC ，tA＜tB＜tC 解析：抛出点距A、B、C点间的高度逐次减小，由公式  可知，运动时间逐次减小，故有：tA＞tB＞tC；：抛出点距A、B、C点的水平距离逐次增大，而时间逐次减小，由公式 可知，平抛初速度逐次增大，故有：vA＜vB＜vC。本题选C。点评：平抛运动的时间只由高度决定，水平位移则由高度和初速度共同决定。 例5．如图5所示，斜面的倾角为θ，放在水平地面上，现从顶点以速度v0平抛一小球，不计空气阻力，重力加速度为g。求小球在飞行过程中离斜面的最大距离s。   解析：如图6所示，可将小球的平抛运动分解为垂直斜面向上的匀变速直线运动和沿斜面向下的匀变速运动，初速度v0沿垂直斜面方向上的分量为：v1= v0 sinθ，加速度g在垂直于斜面方向上的分量为：a=g cosθ。根据分运动各自独立的原理可知，球离斜面的最大距离仅由垂直斜面方向的初速度和加速度决定，当垂直于斜面的分速度减为零时，球离斜面的距离最大。由匀变速直线运动的速度位移关系式  及 可得： 。点评：对运动的分解，通常是从合运动的实际效果确定分运动的方向，但有些问题中，依据问题的特殊情形，结合解题需要确定分运动的方向，可以简化解题过程。 四、类平抛运动 物体被沿某方向以一定初速度抛出，抛出后只在与初速度垂直方向上受到恒定的外力作用，这类运动就是类平抛运动。和平抛运动不同的是，在合外力方向上的分运动不是自由落体运动，其加速度可依据牛顿第二定律求出。一般也是将其分解为初速度方向的匀速直线运动和合外力方向的初速度为零的匀加速直线运动。 例6．如图7所示，光滑斜面长为a，宽为b，倾角为θ。一物块沿斜面从上方顶点P水平射入斜面，而从右下方顶点Q离开斜面。求物块入射的初速度。   解析：由于斜面光滑，被水平抛出的物体在水平方向以初速度做匀速直线运动；在沿斜面向下方向，对物体运用牛顿第二定律有：  ，解得： 。由此可知，沿斜面方向，物体做初速度为零，加速度为的匀加速直线运动。设抛出时的速度为vo，运动时间为t，对物体上述两个方向的运动分别有： ， 。解得： 。点评：这类问题的处理方法与平抛运动相同。 五、圆周运动问题 描述圆周运动的物理量有描述运动快慢的物理量，如周期、线速度、角速度等，有描述速度变化快慢的物理量向心加速度。在匀速圆周运动中，恒定的物理量是周期、角速度，向心加速度、向心力只是大小恒定，方向时刻指向轨道圆心。向心力是作用在匀速圆周运动物体上外力的合力，它和向心加速度间满足牛顿第二定律。 例7．如图8所示，直径为d的纸制圆筒，以角速度ω绕轴O匀速转动，一子弹沿直径穿过圆筒，若子弹在圆筒旋转不到半周时在圆筒上留下a、b两个弹孔，已知ao、bo夹角为 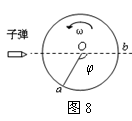 ，求：（1）子弹的速度；（2）若题中“在圆筒旋转不到半周时”去掉，子弹的速度又如何？  解析：（1）子弹从b孔穿出时，第一个弹孔a恰好转到图中的位置，因此，子弹从a穿入到从b穿出圆筒时，圆筒转过的角度为π-φ，(小于π，圆筒旋转不到半周)，则子弹穿过圆筒的时间为：t＝  ，在这段时间内子弹的位移为d，则子弹的速度为：  。（2）当没有“圆筒旋转不到半周”的条件限制时，圆筒旋转的角度有多种可能值：nπ+(π- )，(n为转过的周数，n＝0，1，2，…)，所用时间为t＝ ，则子弹的速度为： (n＝0，1，2，…)。例8．如图9所示的皮带传动装置中，B、C两轮固定在一起绕同一轴转动， A、B两轮用皮带传动，A、B、C三轮的半径关系为rA=rC=2rB。若皮带不打滑，求A、B、C三轮边缘的a、b、c三点的角速度之比及线速度之比。 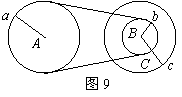  解析：由于皮带不打滑，A、B两轮边沿a、b两点的线速度相等，即  ，由关系 可知，角速度之比为 ；由于B、C两轮固定在同一转轴上转动，边沿上的b、c两点角速度相等，即 ，由关系式可知， 。由以上几式可得： : : =1:2:2， : : =1:1:2例9．如图10所示，长度为0.5m的轻质细杆OA，A端有一质量为3kg的小球，以O点为圆心，在竖直平面内做圆周运动，小球通过最高点时的速度为2m/s，取g=10m/s2.则此时轻杆OA将   A．受到6.0N的拉力 B．受到24N的拉力 C．受到6.0N的压力 D．受到54N的压力 解析：小球过最高点时，轻干处于竖直方向，它对小球若有作用力，作用力的方向肯定也在竖直方向。设小球过最高点时受到竖直向下的拉力为T，对小球过最高点时的运动运用牛顿第二定律有：  。代入数据解得： ，负号说明轻杆对小球作用的是竖直向上的推力，由牛顿第三定律可知，小球对轻杆作用的是向下的压力，大小为6N。本题选C。点评：对于事先不能确定方向的矢量，可假设它可能的某一方向，求解后，依据它的正负再作出判断。 例10．如图11所示，质量为m的小球被细线悬挂在天花板上的O点，在水平面内做匀速圆周运动，运动中细线与竖直方向的夹角为θ，细线长度为l。求小球圆周运动的角速度。   解析：小球运动中受重力mg和细线沿细线斜向上的拉力T的作用。由于小球在水平面上匀速圆周运动，具有沿水平方向指向轨道圆心的加速度，在竖直方向则处于静止状态。因此，在竖直方向对小球运用共点力平衡条件有：  ，在水平方向运用牛顿第二定律有： ，由几何关系有： 。解得小球运动的角速度为： 。点评：向心力是效果力，是指质点所受外力的合力或各力沿轨道半径方向的分力的矢量和。 (责任编辑：admin) |