|
光滑斜面上的动力学 安徽省砀山中学物理组 董凤兰 物体沿光滑斜面运动是每年高考的必考模型，该类试题以受力分析、牛顿运动定律、运动学方程等基本规律为载体，突出考查学生利用数学（几何关系、函数关系）处理物理问题的能力，典型题目有求解最短时间、巧用时间相等两种类型。如图1，光滑斜面倾角为  ，物块受重力 和支持力 ，由牛顿第二定律： ，可得沿斜面向下的加速度： 。 图1 一、求解最短时间 例1．如图2，几个倾角不同的光滑斜面，高度相同，不同的物体从不同斜面的顶端由静止开始滑下，则下列说法中正确的是（ ） A．滑到底端所用的时间相等 B．在倾角为 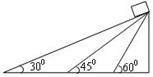 的斜面上滑行时间最短C．在倾角为  的斜面上滑行时间最短 D．在倾角为  、的斜面上滑行时间相等  图2 图3 解析：任找一斜面，如图3，倾角设为 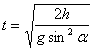，则物体的加速度，斜面高度设为 ，则物体的位移 ，由 ，可得滑行时间 ，可见：一定时，角越大，时间越短，故选C例2．一间新房即将建成要封顶,考虑到下雨时落至房顶的雨滴能尽快淌离房顶,需要设计房顶的高度,设雨滴沿房顶下淌时做无初速度无摩擦的运动,那么图4中所示的四种情况中符合要求的是： （ ）   图4 图5 解析：房子即将建成，所以该题的不变量是斜面的底边长  ，如图5，雨滴的加速度，位移 ，由，可得下淌时间 ，可见：一定， 时，时间最短。故选C二、巧用时间相等 例3．（2004全国Ⅰ15）如图6，aD．bD．cd是竖直面内三根固定的光滑细杆，A．B．C．d位于同一圆周上，a点为圆周的最高点，d点为最低点。每根杆上都套着一个小滑环（图中未画出），三个滑环分别从A．B．c处释放（初速为0），用  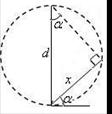、 、 依次表示滑环到达d所用的时间，则 （ ）A．  B．  C． D．   图6 图7 解析：设圆的直径为  ，若沿直径ad下滑，作自由落体运动，由 ，可得： ；若沿任一倾角为的弦下滑，如图7，加速度，位移 ，由，得，所以下滑时间与角无关，故选D变式练习．如图8，o点是竖直圆环的顶点，oc是圆环的直径，oa和ob是两条不同倾角的弦。在oa、ob、oc线上置三个光滑的斜面，一质点从O点自由释放，先后分别沿oa、ob、oc下滑，到圆环上的时间比较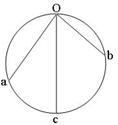：（ ）  图8 A．到a点所用的时间最短 B．到b点所用的时间最短 C．到c点所用的时间最短 D．到a、b、c三点所用的时间一样长 解析：采用与例3类似的方法，可得下滑时间也与 角无关，选D，于是可得到结论：物体沿光滑的弦，从圆周上任一点滑行到圆周最底点，或从圆周最高点滑行到圆周上任一点，所用时间相等，与弦的倾角无关。应用1．在距离坡底为  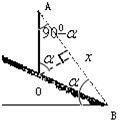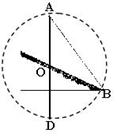的山坡上竖直固定长也为的直杆AO，A端与坡底B间连有一钢丝，钢丝处于伸直状态，一穿心于钢丝上的小球从A点由静止开始沿钢丝无摩擦地滑下，如图9，则小球在钢绳上滑行的时间为（ ）A．   B． C． D．条件不足，无法计算    图9 图10 图11 解析：方法一、如图10，设钢丝倾角为 ，下滑加速度，位移 ，由，得 ，故选B方法二、以  为圆心，为半径画圆，如图11，由结论知从A到B与从A到D时间相等，故 ，得应用2．一质点从倾角为 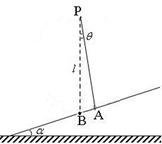的斜面上方P点沿光滑斜槽PA由静止开始下滑，如图12，若要使质点滑至斜面所需的时间最短，则PA与竖直线PB之间的夹角 应取何值？若PB长为，求此最短时间。  图12 图13 解析：如图13，以P为最高点，作一竖直圆周（圆心O一定在竖直线PB上）与斜面相切与A，质点由静止沿光滑斜槽PA下滑至斜面，时间最短。说明如下：在图13中任作另一斜槽PC，若质点沿此槽下滑，由结论知，  ，所以 。由几何关系： 。设圆半径为  ，则 ，由几何关系： ，得 ，由应用1的结果得：
(责任编辑：admin) |