|
宇宙速度的正确认识 江苏省南通市第二中学 陈雅 在天体运动和卫星发射中，宇宙速度是个非常重要的概念。一般教材中都给出了三个宇宙速度的定义和数值：第一宇宙速度（亦称环绕速度）是指物体（卫星）离开地面绕地球做圆周运动所需的最小发射速度，大小为  ；第二宇宙速度(亦称脱离速度)是物体挣脱地球引力的束缚而成为绕太阳运行的人造行星，或飞到其他行星上去的飞船所具有的最小速度，大小为 ；第三宇宙速度(亦称逃逸速度)是物体要进一步挣脱太阳的引力束缚，飞到太阳系以外的宇宙空间去所必须具有的最小速度，大小为 。本文将对这三个宇宙速度的推导过程及所涉及的参考系等问题进行阐述。由于一般教材中都对第一宇宙速度的推导有详细的解释，所以本文对此略过。1．第二宇宙速度的推导 1．1利用功能关系推导 一个航天器在它的燃料烧完后脱离地球的过程中，该系统符合机械能守恒的条件。物体在地面开始运动到脱离地球引力范围（相当于上升到无限远处）的过程中，克服引力做功，动能减少，所以初始动能必须不小于脱离过程中克服引力所做的功。  ………………………………①但同一物体在不同高度处所受地球引力并不相等，随着物体高度的增加，地球引力将逐渐减弱。因此，功的数值不是简单地用  就可以计算的。这里介绍两种方法，一是用元功积分的思想，二是用微分的思想。 方法一：根据万有引力定律，如果用G表示万有引力恒量，M表示地球的质量，m表示物体的质量，r表示物体离地心的距离，R为地球半径。则物体在离地心r处所受地球引力为  ，则在物体上升dr的过程中，克服引力做功为 ……………………………… ②对上式积分，积分限为从R积到∞，  所以，  ………………………………③结合①、③可以得到  ……………………………④把  Nm2/kg2， kg， m带入上式即可计算出第二宇宙速度的大小为 km/s．方法二：如图2所示，设物体m从地球E的引力场中从P0处移动到Pn处。因各处的引力不等，我们可把P0Pn的一段距离分成许多极小的等分Δx。P0、P1、P2、…… Pn和地球中心的距离分别为r0、r1、r2、…… rn；先求出每一等分中的平均引力，然后求出通过每一等分时物体克服地球引力所做的功，这些功的总和，就是物体从P0移动到Pn克服地球引力所做的功。  物体在Pi处所受的引力为  ，因为Pi和Pi+1相距极近，物体在Pi 、Pi+1间所受万有引力的平均值可以近似地等于两处引力的比例中项，即： ；物体从Pi移动到Pi+1’的过程中克服万有引力所做的功为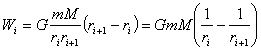：  ；则物体从P0移动到Pn整个过程中克服万有引力所做的功为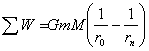：  所以使物体从地球表面r 0=R处出发而脱离地球，即到达rn =∞处，克服引力做功为 ，与方法一推导的结果一致。应该指出，物体从P0处移动到Pn处克服万有引力所做的功，在数值上就等于物体在P0和Pn两处物体与地球组成的系统的重力势能之差，表达式  就表示物体在离地心r处时具有的重力势能。1．2利用动力学方程推导 设物体以初速度  地球表面沿铅垂方向离开地球，地球引力F（为位置坐标的函数） ，初始条件为， ，列运动微分方程  即  ………………………⑤对上式做分离变量的变换，并代入初始条件，进行积分 得  即  …………………………………⑥⑥式表明了物体速度随位置（x）的变化规律。如果 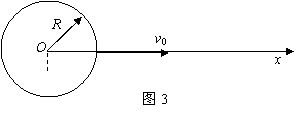 ，则不论x为多大，甚至达无穷大，速度v永远不会为零。可见欲使物体上抛后一去不返，其最小速度（即第二宇宙速）为 km/s。  2．第三宇宙速度的推导 仿照上面推导第二宇宙速度的任一方法，注意到  kg，日地距离 m，并且物体是从地球表面而非太阳表面开始向外运动的，可得到物体脱离太阳系引力的最小速度为 km/s。怎么不是16．7km/s？ 问题在于在研究第二宇宙速度时物体是从地面抛出的，速度是相对于地面而言的，即以地球为惯性系。而在研究第三宇宙速度时，是以太阳为惯性系，所以上面得到的  是相对于太阳的。而地球本身在绕太阳做公转，其公转速度 km/s，如果物体顺着地球运动的轨道切向飞出的话，便可借助于地球的公转线速度，因而只需 ＝42．2－29．8＝12．4 km/s就行了。但是，物体要飞出太阳系，要克服太阳的引力，首先要挣脱地球引力的束缚才行，故物体在地面上应该具有的动能为  所以  ＝16．7km/s。至此我们分析了宇宙速度的推导过程，并明确了宇宙速度均是相对于地球而言的。因此，诸如“地球公转速度29．8km/s比16．7km/s大，为什么地球不离开太阳系？”这样的问题便迎刃而解了。 需要指出的是，在摆脱地球束缚的过程中，在地球引力的作用下物体实际上并不是直线飞离地球，而是按抛物线飞行，脱离地球引力后在太阳引力作用下绕太阳运行。摆脱太阳引力的束缚飞出太阳系时将按双曲线轨迹（相对于地球）飞离地球，而相对太阳来说仍是沿抛物线飞离太阳。 参考文献： 周衍柏编，理论力学教程，高等教育出版社，1996． (责任编辑：admin) |