|
对复振子的定量研究 湖北监利柘木中学 王卫明 摘要:本文从牛顿第二定律出发,导出了振子的运动学方程。 关键词:复振子、牛顿第二定律的应用 一、光滑水平面上运动的复振子 如图一所示,在光滑水平面上,理想轻质弹簧的原长为  建立(惯性参考系) 弹簧上产生的弹力的大小: 根据牛顿第二定律, 对A: 对B: 由(1)(2)两式得: 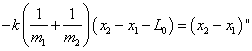 即: 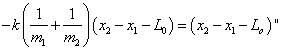 解得: 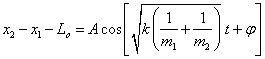 (3) (3)(3)式中:A表示弹簧的最大形变量, 为了使 由于系统所受合外力为0,则 (5)式中: 由(3)(4)(5)解得: 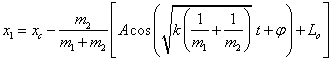 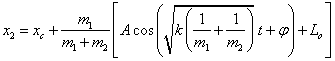 或  (6) (6)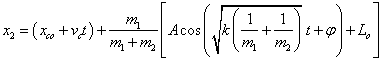 (7) (7)(6)(7)式表明: 1.m1在质心左边  。 。m2在质心右边 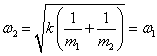 。 。2.m1、m2做简谐振动的相位差为180°。 3.m1、m2的运动可以分解成匀速直线运动和简谐振动。 二、在重力场作用中的复振子 设轻质弹簧的原长为  对A: 对B: 解得: 而在重力场中: 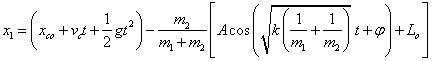 (9) (9)由(8)(9)解得: 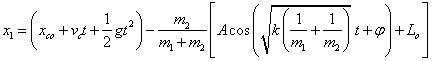 (10) (10)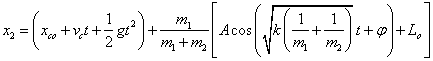 (11) (11)(10)(11)式表明: 1.m1、m2仍相对于质心做简谐振动。 2.m1、m2的运动可以分解成竖直方向的匀变速直线运动和简谐振动。 (责任编辑:admin) |
