|
速度关联问题解法探究 陕西省宝鸡市陈仓区教育局教研室 邢彦君 正确建立连接体间的速度关联关系，是求解连接体有关速度问题的切入点，也是求解有关连接体综合问题的关键。 ［原型问题］如图1-1所示，在一光滑水平面上放一个物体，人通过细绳跨过高处的定滑轮拉物体，使物体在水平面上运动，人以大小不变的速度v运动。当绳子与水平方向成θ角时，物体前进的瞬时速度是多大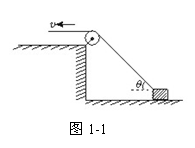？  [解法探究] 解法一：应用微元法求解 设经过短暂时间Δt，则：物体的位移Δs1=BC。如图1-2所示：过C点作CD⊥AB，当Δt→0时，∠BAC极小，在△ACD中，可以认为AC=AD，在Δt时间内，人拉绳子移动的距离Δs2=BD，即为在Δt时间内绳子端点的位移。 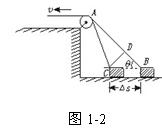 由图可知：BC=  ；由速度的定义知：物体移动的速度为v物= ；人拉绳子的速度，即绳子端点移动的速度v= 解以上三式得：v物=  解法二：应用合运动与分运动的关系求解 绳子牵引物体的运动中，物体实际在水平面上运动，这个运动就是合运动，所以物体在水平面上运动的速度 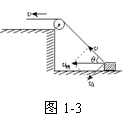 是合速度，选物体（质点）为研究对象，物体也就是绳子端点水平向左的运动造成的效果，一是使滑轮右边的绳子缩短，即使绳收缩；二是使θ变小，使绳绕滑轮顺时针转动。也就是说物体一方面参与沿绳斜向左上的运动，一方面参与垂直于绳斜向左下的运动。这样，物体水平向左运动速度v物可按如图1-3所示进行分解。 由于运动中绳子不发生伸缩及弯曲形变，故有：v=v物cosθ（使绳子收缩），v⊥=v物sinθ（使绳子绕定滑轮上的A点转动）。 解以上两式得：v物= 易错提示：弄不清合运动与分运动，将物体沿水平面的运动当成了分运动，将绳子收缩的速度按图1-4所示分解，从而得出错解v物=v1=vcosθ。 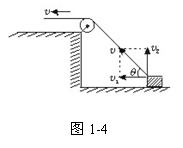 解法三：应用能量转化及守恒定律求解 设当绳子与水平方向成θ角时，人拉绳的力大小是F，由于定滑轮不改变力的大小，所以绳拉物体的力大小也是F。则此时：人对绳子的拉力F对绳子做功的功率为P1=Fv；绳子对物体的拉力F对物体做功的功率为P2=Fv物cosθ。由能量守恒定律可知：P1=P2。 解以上三式得：v物= 。易错提示：计算绳子拉力对物体做功功率时，容易忽视F方向与v方向间的夹角θ。 ［巩固练习］ 1．如图2所示，物体A置于水平面上，A前固定一滑轮B，高台上有一定滑轮D，一根轻绳一端固定在C点，再绕过B、D。BC段水平，当以速度vo拉绳子自由端时，A 沿水平面前进，求：当跨过B的两段绳子夹角为ɑ 时A的运动速度v。（提示：设该时刻拉绳的力大小为F，则BD绳和BC绳拉物体的力大小都是F，拉绳的力的做功功率为 P1=Fvo，BD绳对物体做功的功率为P2=Fvcosɑ ,BC绳对物体做功的功率为Ｐ2/=Fv，由能量守恒可知：P1 =P2+Ｐ2/。答案：vo/（1+cosɑ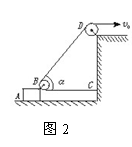））  2．如图3所示，A、B两车通过细绳跨接在定滑轮两侧，并分别置于光滑水平面上，若A车以速度vo向右匀速运动，当绳与水平面的夹角分别为α和β时，B车的速度是多少？（提示：将A的速度向沿绳向下方向与垂直绳斜向上分解，将B的速度沿绳向上方向与垂直绳斜向下分解。答案：vB=vAcosβ/cosɑ）  3．如图4所示，均匀直杆上连着两个小球A、B，不计一切摩擦。当杆滑到如图位置时，B球水平速度为vB，杆与竖直夹角为α，求此时A球速度大小。（提示与答案：将A球竖直向下的速度向沿杆向下和垂直杆斜向下分解，将B球水平向右的速度向沿杆向下和垂直杆斜向上分解。答案：vBtanɑ）  ［拓展训练］ 1．一辆车通过一根跨过定滑轮的绳PQ提升井中质量为m的物体，如图5所示。绳的P端拴在车后的挂钩上，Q端拴在物体上．设绳的总长不变，绳子质量、定滑轮的质量和尺寸、滑轮上的摩擦都忽略不计。开始时，车在A点，左右两侧绳都已绷紧并且是竖直的，左侧绳绳长为H。提升时，车加速向左运动，沿水平方向从A经B驶向C。设A到B的距离也为H，车过B点时的速度为vB。求在车由A移到B的过程中，绳Q端的拉力对物体做的功。（提示：将车的速度沿绳斜向下与垂直绳斜向上分解，以被拉物体为研究对象，运用动能定理或功能原理。答案 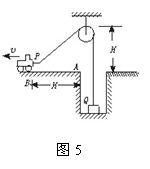 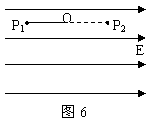）    2．一带正电的小球，系于长为L的不可伸长的轻线一端，线的另一端固定在O点，它们处在方向水平向右电场强度大小为E的匀强电场中。已知电场对小球的作用力大小等于小球的重力。现把小球拉到图6中的P1处，使线绷直，并与电场方向平行，然后由静止释放小球。已知小球在经过最低点的瞬间，因受线的拉力作用，速度的竖直分量突变为零，水平分量没有变化，则小与球到达P1等高的P2点时的速度的大小为多少？（提示：小球从释放到经过最低点，作出速度为零的云加速运动，将小球过最低点时的速度沿竖直向下与水平向右分解，小球由最低点向P2点运动过程中，对小球运用动能定理或功能原理。答案：  ）
(责任编辑：admin) |