|
用三角形法则求解三力平衡问题 陕西省宝鸡市陈仓区教育局教研室 邢彦君 物体在几个共点力作用下处于静止状态或匀速直线运动状态,作用在物体上的这几个力的合力为零。若物体在三个共点力的作用下处于静止或匀速直线运动状态,这三个力的合力必为零,此时可运用三角形法则进行分析与求解。 一、三角形法则 三个共点力的合力为零时,若用平行四边形定则求出任意两力的合力,这个合力将代替原来的两个力,这样,三力平衡问题就变成了二力平衡问题,合力与第三个力大小相等、方向相反、作用在同一条直线上。因此,若将表示三个力的矢量平行移动,使其依次首尾相接,将构成封闭三角形。这就是求解与分析三个共点力平衡问题的三角形法则。运用三角形法则作出表示力矢量的三角形后,可利用解三角形的知识与方法进行分析与求解。 例1.如图1所示,一个半球形的碗放在桌面上,碗口水平,O点为其球心,碗的内表面及碗口是光滑的。一根细线跨在碗口上,线的两端分别系有质量为m1和m2的小球,当它们处于平衡状态时,质量为m1的小球与O点的连线与水平线的夹角为α=60°。则小球的质量比m2/m1为 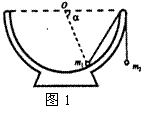 A. 解析:选碗中的小球m1为研究对象,如图2所示,由于碗的内表面光滑,它受竖直向下的重力mg、从m1(质点)指向球心O的支持力N(弹力)、沿细线斜向上的拉力T(弹力)三个力的作用而处于静止状态,由力的平衡条件可知,它们的合力为零,故将表示这三个力的矢量平行移动依次首尾相接,将构成封闭三角形,如图3所示。由正弦定理有: 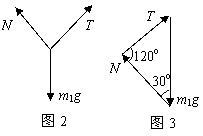 二、求解动态平衡问题 物体在三个共点力的作用下处于静止状态或匀速直线运动状态,若其中的一个力缓慢变化,而物体仍处于静止状态或匀速直线运动状态,这类问题就是动态平衡问题,变力变化过程中的每一个状态,三力的合力都等于零。这类问题中至少有一个大小、方向均保持不变,三力矢量构成的封闭三角形中,至少有一个边保持不变,即三角形的两个顶点将保持不动,根据题中变力的变化情况,可确定出另一顶点的变化,由此可以判断出变力的变化情况。 例2.如图5所示,质量为m的小球用细线悬于天花板上。在小球上作用水平拉力F,使细线与竖直方向保持θ角,小球保持静止状态。现让力F缓慢由水平方向变为竖直方向。这一过程中,小球处于静止状态,细线与竖直方向夹角不变。则力F的大小、细线对小球的拉力大小如何变化?  解析:由于小球始终保持静止状态,小球受的重力mg、水平拉力F和细线拉力T三个矢量将组成封闭三角形,如图5所示。由于重力mg大小及方向均不变,三角形的两个顶点(矢量mg的首尾)固定不动;由于θ角保持不变,即表示细线拉力T的边方向不变,当F由水平逐渐变竖直时,力矢量F与力矢量T的交点,三角形的另一顶点将沿矢量T逐渐向上滑移,由图可以看出表示力矢量F的边先是逐渐变小,当与细线垂直时有最小值,接着逐渐变大。这一过程中,表示细线拉力T的边一直减小到零。 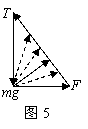 故,力F先逐渐减小再逐渐增大,细线的拉力一直减小。 (责任编辑:admin) |
