|
精挑细选 对症下药 ──匀变速直线运动公式的选择技巧 江苏省靖江市季市中学 范晓波 匀变速直线运动部分涉及的公式与规律很多，怎样才能快速选出符合解题要求的公式和规律，是许多高一学生迫切希望解决的问题。现从个人的经验出发，介绍一下匀变速直线运动规律选择的原则和方法。 一、运动规律的分类 熟悉各条规律的形式和使用前提是熟练使用规律的第一步，只有在条理清晰后我们的记忆才能既快又准，而且记得长久。按照涉及的物理量和规律的来源，可将所有匀变速直线运动的规律进行如下分类： 第一组：  可统称为基本公式，由三个表达式组成，各式中均含初速度  、加速度 两个常量。原则上利用它们已经可以解决所有的运动学问题，但很多时候使用并不方便，该组公式往往是我们最后的选择。第二组：  可统称为平均速度关系式，由两个表达式组成，两式中均没有出现加速度 ，由此可见，它是解决不直接涉及加速度的运动问题的最佳选择。第三组：  可统称为特殊推论，由三个表达式组成，分别对应中间时刻、中间位置、相邻相等的时间间隔这些特殊位置或过程。 第四组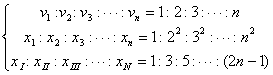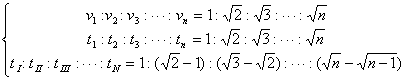：     可统称为比例规律，由六个比例式组成，分别对应于  的匀加速直线运动过程按时间等分和按距离等分的情况。对末速度 的匀减速直线运动，利用“过程反演”变换成反方向的匀加速直线运动后同样适用。二、选择的原则与顺序 规律选择得是否恰当将直接影响到解题的难易程度和准确性。按方便、简洁、准确的原则，运动规律的选择顺序一般为： 比例规律→特殊推论→平均速度关系式→基本公式 从左往右，优先程度逐渐降低。复杂的匀变速直线运动问题，可能需要将几组规律交叉使用。 下面分别举例说明： 例：矿井里的升降机，由静止开始匀加速上升，经  速度达到 后，又以这个速度匀速上升 ，然后匀减速上升，经过 停在井口，求矿井的深度。分析：升降机共经历三个运动阶段，其中一、三两个运动阶段存在加速度，但题干中没有提供具体数值，待求量中也没有加速度，符合第二组公式的特点。 解：运动过程如图所示，设三个运动阶段的位移大小分别为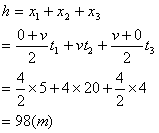  、 、 由匀变速直线的运动规律和匀速直线运动的位移公式 得：  说明：此类不明显涉及加速度的问题，应优先考虑使用平均速度关系式处理。整个处理过程简洁流畅，还可避免在加速度方向上出现错误。若能结合  图像分析，更是如虎添翼。例：一质点沿AD直线作匀加速直线运动，如图，测得它在AB、BC、CD三段的时间均为t，测得位移AC=L1，BD=L2，试求质点的加速度？  分析：AB、BC、CD是三段相邻相等的时间间隔，符合特殊推论中位移差规律使用的条件。唯一不足的是L1、L2并非相邻相等的时间间隔内位移之差，必须通过数学变换得到  。解：设  、 、 则：  两式相加：  由图可知：  则：a =  说明：审题过程中抓住关键性词句，从而找出运动过程的特点及涉及哪些运动学量，是有针对性选择运动规律的依据，尤其是在运用特殊推论解决问题时更应如此。 例：一个小球从距地面高度为 h的某点由静止开始落下，不计空气阻力，最后  通过的路程为全程的 ，则h的大小为多少？分析：自由落体运动是初速度为零的匀加速直线运动，所以应优先考虑使用比例规律处理。 解：在自由落体运动的第1s内、第2s内……第5s内位移大小之比为  题中已经给出最后1秒通过的路程为全程的 ，故小球下落的总时间 所以  说明：对初速度为零的匀加速直线运动或末速度为零的匀减速直线运动，利用比例规律处理最方便，但对规律本身的理解、记忆要求较高。 例：一个物体以一定的初速度做匀加速直线运动，匀加速过程共持续了  ，该过程中的第一个 内物体通过 的位移，最后的内物体通过 的位移，求物体在内的总位移。分析：已知两个中间过程的位移和时间，用位移除以时间可先求出这两个过程对应的平均速度，按特殊推论中的中间时刻速度公式，也就找到了两个时刻的瞬时速度，结合基本公式就能求出加速度a与初速度v0,余下问题迎刃而解。 解：运动过程如图所示 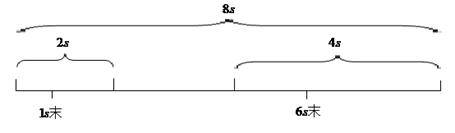 由  可得：  从1s末到6s末，由  得： 从开始到1s末，同理：  所以  说明：由于 、两个常量均未知，直接用基本公式求解需列方程组，但从过程特点出发，利用特殊推论找到两个时刻的速度后再结合基本公式求解，处理和运算过程就变得很简单。总之，在学习中注意不要死记硬背公式和规律。重要的是领会公式与规律的来龙去脉及其特点，要通过一些具体实例，培养一题多解的思想，并且能够在解题时选择最简单的方法，从而切实加深对规律的选择原则和方法的理解，这样的学习就不仅仅是知识的堆砌，而是能力的增长，素质的提高。 三、变式练习： 1．一辆汽车在笔直的公路上做匀变速直线运动，该公路每隔  安置一个路标，如图所示，汽车通过AB两相邻路标用了 ，通过BC两相邻路标用了 ，求汽车通过A、B、C三个路标时的速度。 2．一个做匀加速直线运动的物体，连续通过两段长为L的位移所用的时间分别为t1、t2，求物体的加速度？ 3．一个物体以一定的初速度做匀加速直线运动，第一个2s通过12m的位移，第四个2s通过72m，求：（1）物体的初速度；（2）物体的加速度；（3）物体在前8s内的位移。 4．一物体由静止开始做匀加速直线运动，在第49 s内位移是48．5m，,则它在第1s内、第60s内、前60s内的位移分别是多少？ 5．一物体从斜面顶端由静止开始匀加速下滑，它在最初3s内的位移为x1，最后3s内的位移为x2，若x2-x1=6m，x1：x2=3：7，求斜面的长度为多少？ 变式练习答案： 1．  ； ； 2．  3．（1）  （2） （3） 4．  ； ； 5． 
(责任编辑：admin) |