|
2.3双曲线 重难点：建立并掌握双曲线的标准方程，能根据已知条件求双曲线的标准方程；掌握双曲线的简单几何性质，能运用双曲线的几何性质处理一些简单的实际问题． 经典例题：已知不论b取何实数，直线y=kx+b与双曲线  总有公共点，试求实数k的取值范围．当堂练习： 1．到两定点  、 的距离之差的绝对值等于6的点 的轨迹 （ ）A．椭圆 B．线段 C．双曲线 D．两条射线 2．方程  表示双曲线，则 的取值范围是 （ ）A．  B． C． D． 或 3． 双曲线  的焦距是 （ ）A．4 B．  C．8 D．与 有关4．已知m,n为两个不相等的非零实数，则方程mx－y+n=0与nx2+my2=mn所表示的曲线可能是 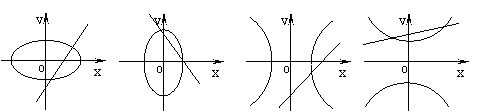（ ）  A B C D 5． 双曲线的两条准线将实轴三等分，则它的离心率为 （ ） A．  B．3 C． D．  6．焦点为  ，且与双曲线 有相同的渐近线的双曲线方程是 （ ）A．  B． C． D． 7．若  ，双曲线 与双曲线 有 （ ）A．相同的虚轴 B．相同的实轴 C．相同的渐近线 D． 相同的焦点 8．过双曲线  左焦点F1的弦AB长为6，则 （F2为右焦点）的周长是（ ）A．28 B．22 C．14 D．12 9．已知双曲线方程为  ，过P（1，0）的直线L与双曲线只有一个公共点，则L的条数共有 （ ）A．4条 B．3条 C．2条 D．1条 10．给出下列曲线：①4x+2y－1=0; ②x2+y2=3; ③  ④ ，其中与直线y=－2x－3有交点的所有曲线是 （ ） A．①③ B．②④ C．①②③ D．②③④ 11．双曲线  的右焦点到右准线的距离为__________________________．12．与椭圆  有相同的焦点，且两准线间的距离为 的双曲线方程为____________．13．直线  与双曲线 相交于 两点，则 =__________________．14．过点  且被点M平分的双曲线 的弦所在直线方程为 ．15．求一条渐近线方程是  ，一个焦点是 的双曲线标准方程，并求此双曲线的离心率． 16．双曲线  的两个焦点分别为 ， 为双曲线上任意一点，求证： 成等比数列（ 为坐标原点）．17．已知动点P与双曲线x2－y2＝1的两个焦点F1，F2的距离之和为定值，且cos∠F1PF2的最小值为－. （1）求动点P的轨迹方程； （2）设M(0，－1)，若斜率为k(k≠0)的直线l与P点的轨迹交于不同的两点A、B，若要使|MA|＝|MB|，试求k的取值范围． 18．某中心接到其正东、正西、正北方向三个观测点的报告：正西、正北两个观测点同时听到了一声巨响，正东观测点听到的时间比其他两观测点晚4s. 已知各观测点到该中心的距离都是1020m. 试确定该巨响发生的位置.(假定当时声音传播的速度为340m/ s :相关各点均在同一平面上). 参考答案： 经典例题：[解析]：联立方程组  消去y得(2k2－1)x2+4kbx+（2b2+1）=0,当  若b=0，则k ；若 ，不合题意.当  依题意有△=(4kb)2－4(2k2－1)(2b2+1)＞0， 对所有实数b恒成立， ∴2k2<1，得 .当堂练习： 1.D; 2.D; 3.C; 4.C; 5.B; 6.B; 7.D; 8.A; 9.B; 10.D; 11.  ; 12.  ; 13.  ;14.  ;15．[解析]：设双曲线方程为：  ，∵双曲线有一个焦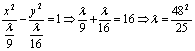点为（4，0）， 双曲线方程化为：  ，∴双曲线方程为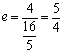：  ∴ ．16．[解析]：易知  ，准线方程： ，设 ，则  ， ， ，   成等比数列.17． [解析]：(1)∵x2－y2＝1，∴c＝.设|PF1|＋|PF2|＝2a(常数a＞0)，2a＞2c＝2，∴a＞ 由余弦定理有cos∠F1PF2＝＝＝－1 ∵|PF1||PF2|≤()2＝a2，∴当且仅当|PF1|＝|PF2|时，|PF1||PF2|取得最大值a2. 此时cos∠F1PF2取得最小值－1，由题意－1＝－，解得a2＝3，   ∴P点的轨迹方程为＋y2＝1.(2)设l：y＝kx＋m(k≠0)，则由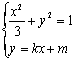，  将②代入①得：(1＋3k2)x2＋6kmx＋3(m2－1)＝0 (*)设A(x1，y1)，B(x2，y2)，则AB中点Q(x0，y0)的坐标满足：x0＝ 即Q(－) ∵|MA|＝|MB|，∴M在AB的中垂线上， ∴klkAB＝k·＝－1 ，解得m＝ …③ 又由于(*)式有两个实数根，知△＞0， 即 (6km)2－4(1＋3k2)[3(m2－1)]＝12(1＋3k2－m2)＞0 ④ ，将③代入④得 12[1＋3k2－()2]＞0，解得－1＜k＜1，由k≠0，∴k的取值范围是k∈(－1，0)∪(0，1). 18．[解析]：以接报中心为原点O，正东、正北方向为x轴、y轴正向，建立直角坐标系.设A、B、C分别是西、东、北观测点，则A（－1020，0），B（1020，0），C（0，1020） 设P（x,y）为巨响为生点，由A、C同时听到巨响声，得|PA|=|PB|，故P在AC的垂直平分线PO上，PO的方程为y=－x，因B点比A点晚4s听到爆炸声，故|PB|－ |PA|=340×4=1360 由双曲线定义知P点在以A、B为焦点的双曲线  上， 依题意得a=680, c=1020，  用y=－x代入上式，得  ，∵|PB|>|PA|,  ,答：巨响发生在接报中心的西偏北45°距中心 处. (责任编辑：admin) |