|
有心曲线直径三角形的一个性质及应用 湖北省阳新县高级中学 邹生书 我们把经过有心二次曲线中心的弦叫做直径，把顶点在有心曲线上且有一边是直径的三角形叫做有心曲线的直径三角形.本文向读者介绍有心曲线直径三角形的一个重要性质及其应用. 性质1 已知  是椭圆 的任一直径，点 是椭圆上任意一点，若直线 的斜率都存在，则 .证明 设  ，因为是椭圆的直径，所以点 的坐标为 ，所以  .又因为点在椭圆上，所以有 .两式相减得， ，所以 ，所以.同理可证双曲线也有如下类似性质： 性质2 已知 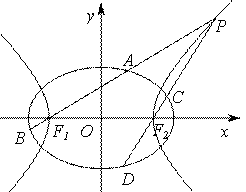是双曲线 的任一直径，点是双曲线上任意一点，若直线的斜率都存在，则 . 图1 例1（2010年高考山东理科卷的第21题）如图1，已知椭圆 的离心率为 ，以该椭圆上的点和椭圆的左右焦点为顶点的三角形的周长为 ，现有一等轴双曲线，其顶点是该椭圆的焦点，设为该双曲线上异于顶点的任意一点，直线 和 与椭圆的交点分别为 和 .(1)求椭圆和双曲线的标准方程； (2)设直线 和的斜率分别为 ，证明: ；(3)是否存在常数  ，使得 恒成立？若存在，求的值；若不存在，请说明理由.本题主要考查椭圆、双曲线的基本概念和基本性质，考查直线和椭圆的位置关系，考查定值和存在性等知识，考查数形结合思想和探究问题的能力. 解(1)椭圆方程为  ，双曲线方程为 （过程略）；（2）过程略；（3）假设存在这样的常数 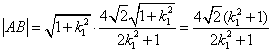，使得恒成立.将直线 的方程 代入椭圆方程整理得， .则  .由弦长公式得， .同理 ，由得 ，将其代入得 .由得， ，即  ，所以 ，故 .本题第二问的结论即双曲线直径三角形的性质为第三问的解答起到了引领解题思路简化运算的台阶作用，如果没有第二问的台阶铺垫，则第三问定值探究的切入变得艰难和茫然，运算由于变量增多导致运算复杂量大难以驾驭而无功而返.下面两题没有台阶铺垫，若有模识别意识自觉运用有心曲线直径三角形的性质解题，则可达到化难为易事半功倍之效. 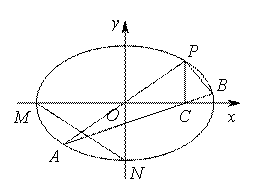 图2 例2(2011年高考江苏卷理科第18题)如图2，在平面直角坐标系  中， 分别是椭圆 的顶点，过坐标原点的直线交椭圆于 两点，其中点在第一象限，过作 轴的垂线，垂足为 .连接 屏延长交椭圆于点.设直线 的斜率为 .（1）当直线 平分线段 时，求的值；（2）当  时，求点到直线的距离 ；（3）对任意的  ，求证: .解（3）(证  )设 ，则 ， .因为直径，由椭圆直径三角形性质得， ，而 ， 所以  ，所以 ，因此，所以.例3 如图3，已知 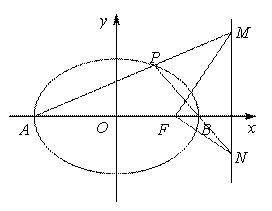是椭圆的左右顶点，点是椭圆上异于的任意一点，（1）直线分别交右准线 于两点，以为直径的圆过右焦点 ；(2)存在垂直于轴的定直线 ，若直线交直线于两点且以为直径的圆过右焦点，则直线为右准线. 图3 证明 （1）设直线 的斜率分别为，由椭圆直径三角形性质得 .则直线的方程为: ①，直线  的方程为: ②，又右准线的方程为； ③.解①③得点  的坐标为 ，解②③得点 的坐标为 .于是 ，所以  ，所以 ，故以为直径的圆过右焦点.（2）设直线 的斜率分别为，由性质得.则直线的方程为：①，直线的方程为:②，设直线的方程为： ③.解①③得点 的坐标为 ，解②③得点的坐标为 .于是 .因为以为直径的圆过右焦点，所以，所以 ，即 ，所以 ，化简得 ，所以 ，于是 ，故直线为右准线.例4（2009年高考福建卷理科第19题）已知 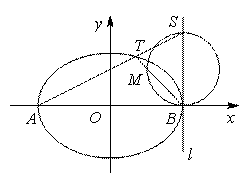分别为曲线 与轴的左右两个交点，直线过点，且与轴垂直， 为上异于点的一点，连结 交曲线于点 .(1)若曲线为半圆，点为圆弧 的三等分点，试求出点的坐标；（2）如图4，点是以 为直径的圆与线段 的交点，试问：是否存在 ，使得 三点共线？若存在，求出的值；若不存在，请说明理由. 图4 解（1）略；（2）假设存在这样的 ，使得三点共线. 设直线  斜率分别为，则直线 的方程为①，又直线的方程为 ②，解①②得点的坐标为 ，所以 ③.因为为圆 的直径，所以 ，所以 ，所以 ④.又由椭圆直径三角形性质知 ，所以 ⑤，将③⑤代入④得， ，所以 ，故存在 ，使得三点共线.用“研究”的态度去对待我们遇到的每一个数学问题，去研究它、解剖它最终对问题达到较为透彻的理解，揭示问题的“通性”，寻找解决问题的“通法”和“优美解”，并用我们所得的通性通法去指导我们的解题实践，这对我们提高解题能力是大有裨益的. (责任编辑：admin) |