|
用双曲线的定义解题 广东省中山一中高中部 许少华 双曲线的定义是双曲线的重要概念，对它的准确理解与正确运用对学好双曲线甚至整个圆锥曲线都很有意义；因此，本文揭示它的应用，谈用双曲线的定义解题。 1.抓定点，用定义 例1 设双曲线与椭圆  有共同的焦点，且与椭圆相交，一个交点 的纵坐标为 ，求双曲线的方程。简解：设所求方程为  由已知得两焦点分别为  、点 则  得 ，由于 得 ，因此方程 为所求。点评：双曲线上的点必满足双曲线的定义，本题抓住“交点 ”满足第一定义，从而应用第一定义求出了双曲线方程中的基本量，显然它比其它方法要简单、方便；2.借图形，用定义  例2 如图，双曲线 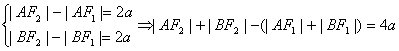其焦点为 ，过 作直线交双曲线的左支于 两点，且 ，则 的周长为 。简解：由  又由  ，  那么 的周长为 点评：图形，具有直观性；本题借助图形，利用第一定义，首先求出  ，尔后，再求周长，显然是求解问题的一种策略；假若本题未给图形，条件“过作直线交双曲线的左支于两点”中，再去掉“左支”两字，情况就大不相同，请试一下。3.抓准线，用定义 例3 已知双曲线以直线  为右准线，离心率为2，且经过定点 ，求实半轴最大时的双曲线方程简解：如图，设右焦点为 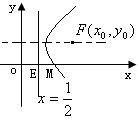 ，由第二定义得 ，即   ，由此得 又  从而 当  时， ，此时方程为 点评：“准线”是用第二定义的重要特征，本题抓住“准线”、设出焦点，用第二定义巧妙产生右焦点的轨迹方程是重点，抓住变量的有界性及基本量间的关系产生  的范围是难点；抓住重点，突破难点是求解的关键。4.抓定值，用定义 例4、某中心接到其正东、正西、正北方向三个观测点的报告：正西、正北两个观测点同时听到了一声巨响，正东观测点听到该巨响的时间比其他两观测点晚 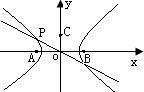 ，已知各观测点到该中心的距离都是 ，试确定该巨响发生的位置。（假定当时声音传播的速度为 ；相关各点均在同一平面内） 简解：如图，以接报中心为原点，正东、正北分别方向为  、 轴的正向建立直角坐标系，设 分别为西、东、北观测点，则 设 为巨响发生点，则 ，由第一定义知 ， ，得 方程为 由  同时听到巨响声，得 ，因此 在直线 上再由  因为  ，得 ，即 ，此时  故巨响发生在接报中心的西偏北  距中心 处。点评：本题抓住“正东观测点听到该巨响的时间比其他两观测点晚 ”想到差为定值，进一步想到双曲线，使其转化为双曲线问题进行求解。5.抓合作，用定义 例5、已知双曲线过点  ，它的一个焦点是抛物线 的焦点 ，求它到另一焦点到轴的距离的最大值。简解：由于  且在双曲线上，得 （1）若  即点 在线段 的中垂线上，它到轴的距离为1；（2）若  即点 在以为焦点且长轴长为10的椭圆上，得方程为 由 ，此时，到轴的距离的最大值为6；综合（1）、（2）知 到轴的距离的最大值为6；评注：从双曲线定义出发产生两种情形，第二种情形又紧紧抓住椭圆定义得到椭圆方程，由方程产生结果；此题中两定义的“和平共处、团结合作”是求解的关键。 6.抓特征，用定义 例6、解方程  简解：原方程可变为  ，令 则方程以变为  显然，点 在以 ， 为焦点，实轴长为 的双曲线上，易得其方程为由  得 点评：本题的一个重要特征是，差为定值2。由此出发，引入 ，使问题很巧妙的转化为几何问题，再结合双曲线的第一定义使问题获解，可以看出这种解法具有创造性。至此可以看出：双曲线的定义是一个内涵十分丰富，应用非常广泛的重要概念；其实，椭圆、抛物线又何尝不是呢？建议你建立在拙文的基础上，结合类比联想来看一下涉及椭圆、抛物线的定义会有哪些问题，也许你进入了一个妙趣横生的新天地。 (责任编辑：admin) |