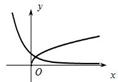
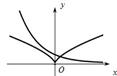
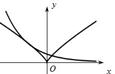
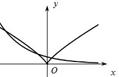
|
与函数有关的两类转化思想 内蒙古赤峰市翁牛特旗乌丹一中 熊明军 高中数学中所遇到的各类函数大致都可以分解为五类基本初等函数：多项式函数、指数函数、对数函数、幂函数以及三角函数。而高中数学中经常遇到的方程（或函数零点）问题、不等式问题又都可以运用转化思想将这两类问题转变成函数问题，然后再利用数形结合加以解决。 ①方程（或函数零点个数）问题  两个函数图象的交点问题（方程与函数）；【解说：】对于由多个基本初等函数融合而成的较复杂方程，我们无法利用解方程的常规方法加以求解，此时不妨将该方程分解为几个简单的基本初等函数，在同一坐标系下作出各函数的图象，数形结合，把方程问题转化为函数图象的交点问题。 【例如：】已知方程  ，求方程两根之和（或已知函数 ，求函数零点个数）。【解析：】这显然是一个无法用常规解方程就能解决的问题，考察该函数可知，将该方程变形得 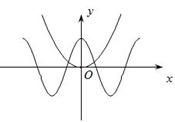 ，可以转化为函数 与函数 的交点问题。在同一个坐标系下作出它们的图象： 由图象可知两函数的交点有两个，并且横坐标互为相反数，则有  。②不等式问题 两个函数图象的位置关系问题（不等式与函数）；【解说：】对于由多个基本初等函数融合构成的不等式，我们也能将其分解为几个基本初等函数，然后在同一坐标系下作出各函数图象，数形结合，把不等式问题转化为函数图象的位置关系（一段图象在另一段图象上  或下 ）。【例如：】求不等式  的解集。【解析：】利用不等式的性质可以解这个不等式，除此方法外，将该不等式变形得  ，可以转化为函数 与函数 图象的位置关系问题。在同一个坐标系下作出它们的图象： 在  和 上 图象都在 图象上面，知不等式解集为 。③综合运用上述两类转化思想解题。 【例如：】作出函数  的图象。【解析：】对高中生来说，该函数是一个比较复杂的函数，这个函数含有两类基本初等函数——指数函数、对数函数，因此，用常规作图方法来解决此问题就变得相当棘手。我们不妨利用上述两类转化思想加以解决： 第一步：将函数 进行分解，得到指数函数 ，幂函数 ；第二步：考察函数 与 轴的交点情况（函数零点个数及大致位置）在同一坐标系下指数函数图象与幂函数图象的交点情况；第三步：确定函数图象在相应区间上的变化趋势 确定 的正负（函数与函数图象的位置关系）。指数函数 与幂函数图象交点情况一览表（其中 为即约分数）：
下面我们举出一个具体的例子来研究： 2010年普通高等学校招生全国统一考试（山东卷）（11）函数  的大致图像。第一步：将函数  进行分解，得到指数函数 ，幂函数；第二步：考察函数 与轴的交点情况，即 在同一坐标系下指数函数图象与幂函数图象的交点情况； 查表的图像（如上图），由图可知 与交点有三个，且横坐标 满足 。即函数的零点有三个，分别是。第三步：确定函数图象在相应区间上的变化趋势 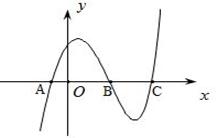确定的正负（函数与函数图象的位置关系）。①在  ：图象在图象下面 ，即图象在轴下方；②在  ：图象在图象上面 ，即图象在轴上方；③在  ：图象在图象上面，即图象在轴下方；④在  ：图象在图象上面，即图象在轴上方。综上所述，函数 的大致图像为： 参考文献： 王久成 朱立明，关于一道高考题的深刻思考，《中学数学教学参考》，2011年第5期 (责任编辑：admin) |
|||||||||||||||||||||||||||||||||||||
有一交点；
没有交点。
