椭圆与双曲线的对偶性质之椭圆篇(1)
杨志明
1.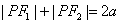
2.标准方程: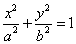
3.
4.点P处的切线PT平分△PF1F2在点P处的外角.
5.PT平分△PF1F2在点P处的外角,则焦点在直线PT上的射影H点的轨迹是以长轴为直径的圆,除去长轴的两个端点.
6.以焦点弦PQ为直径的圆必与对应准线相离.
7.以焦点半径PF1为直径的圆必与以长轴为直径的圆内切.
8.设A1、A2为椭圆的左、右顶点,则△PF1F2在边PF2(或PF1)上的旁切圆,必与A1A2所在的直线切于A2(或A1).
9.椭圆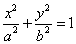 (a>b>o)的两个顶点为 (a>b>o)的两个顶点为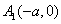 , ,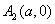 ,与y轴平行的直线交椭圆于P1、P2时A1P1与A2P2交点的轨迹方程是 ,与y轴平行的直线交椭圆于P1、P2时A1P1与A2P2交点的轨迹方程是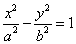 . .
10.若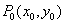 在椭圆 在椭圆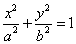 上,则过 上,则过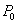 的椭圆的切线方程是 的椭圆的切线方程是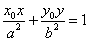 . .
11.若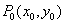 在椭圆 在椭圆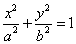 外 ,则过Po作椭圆的两条切线切点为P1、P2,则切点弦P1P2的直线方程是 外 ,则过Po作椭圆的两条切线切点为P1、P2,则切点弦P1P2的直线方程是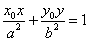 . .
12.AB是椭圆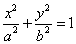 的不平行于对称轴且过原点的弦,M为AB的中点,则 的不平行于对称轴且过原点的弦,M为AB的中点,则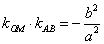 . .
13.若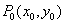 在椭圆 在椭圆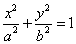 内,则被Po所平分的中点弦的方程是 内,则被Po所平分的中点弦的方程是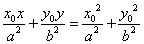 . .
14.若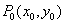 在椭圆 在椭圆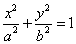 内,则过Po的弦中点的轨迹方程是 内,则过Po的弦中点的轨迹方程是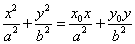 . .
15.若PQ是椭圆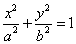 (a>b>0)上对中心张直角的弦,则 (a>b>0)上对中心张直角的弦,则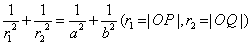 . .
16.若椭圆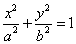 (a>b>0)上中心张直角的弦L所在直线方程为 (a>b>0)上中心张直角的弦L所在直线方程为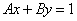 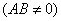 ,则(1) ,则(1) 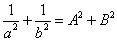 ;(2) ;(2) 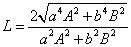 . .
17.给定椭圆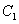 : : (a>b>0), (a>b>0), 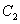 : :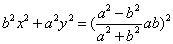 ,则(i)对 ,则(i)对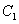 上任意给定的点 上任意给定的点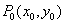 ,它的任一直角弦必须经过 ,它的任一直角弦必须经过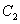 上一定点M( 上一定点M(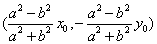 . .
(ii)对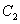 上任一点 上任一点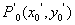 在 在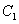 上存在唯一的点 上存在唯一的点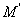 ,使得 ,使得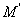 的任一直角弦都经过 的任一直角弦都经过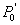 点. 点.
18.设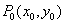 为椭圆(或圆)C: 为椭圆(或圆)C: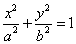 (a>0,. b>0)上一点,P1P2为曲线C的动弦,且弦P0P1, P0P2斜率存在,记为k1, k 2, 则直线P1P2通过定点 (a>0,. b>0)上一点,P1P2为曲线C的动弦,且弦P0P1, P0P2斜率存在,记为k1, k 2, 则直线P1P2通过定点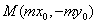 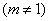 的充要条件是 的充要条件是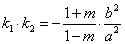 . .
19.过椭圆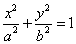 (a>0, b>0)上任一点 (a>0, b>0)上任一点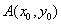 任意作两条倾斜角互补的直线交椭圆于B,C两点,则直线BC有定向且 任意作两条倾斜角互补的直线交椭圆于B,C两点,则直线BC有定向且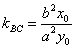 (常数). (常数).
20.椭圆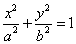 (a>b>0)的左右焦点分别为F1,F 2,点P为椭圆上任意一点 (a>b>0)的左右焦点分别为F1,F 2,点P为椭圆上任意一点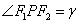 ,则椭圆的焦点角形的面积为 ,则椭圆的焦点角形的面积为
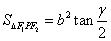 , ,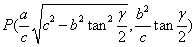 . .
(责任编辑:admin) |
