|
对二元一次不等式确定平面区域的探究 湖北省阳新县高级中学 邹生书 人教版高二数学第二册(上)二元一次不等式确定平面区域属于新增内容,大纲要求是:了解二元一课次不等式的几何意义,能用平面区域表示二元一次不等式(组)。笔者对这部内容作了一些研究,本文将得出的重要结论及其在解题中的应用与大家进行交流,希望能对这节内容的教学和学习有所帮助。 命题1:已知二元一次函数 ①点P1(x1,y1)在直线Ax+By+C=0上 ②若B≠0,则有 点P1(x1,y1)在直线Ax+By+C=0上方 点P1(x1,y1)在直线Ax+By+C=0下方 ③若A≠0,则有 点P1(x1,y1)在直线Ax+By+C=0右方 点P1(x1,y1)在直线Ax+By+C=0左方 分析:①易证,②、③证法类似,下面对②进行证明。 证明:②当B≠0,直线 设P1(x1,y1)是坐标平面内不在l上的任意一点,作直线x=x1交l于点P0,设P0的坐标为(x1,y0). 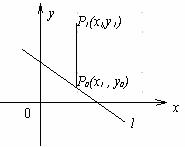 ∵ 点 ∴ 即 点 点 根据这个命题不难得出直线l同侧上的两个点对应的二元函数的值符号相同,异侧上的两个点对应的二元函数值符号相反,即有如下结论: 命题2:已知二元一次函数 ①点 ②点 应用举例: 1、快速准确地确定二元一次不等式所表示的平面区域. 例1:(人教版高二数学第二册第64页例1)画出不等式 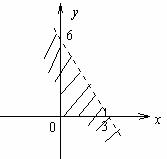 解法1: 解法2: 小结:二元一次不等式确定平面区域的方法: ①点判别法:直线定边界,一点定区域,合则在,不合则不在; ②B符号判别法:直线定边界,符号定区域,同上异下; ③A符号判别法:直线定边界,符号定区域,同右异左. 由例1可知,教材采用点判别法,需要取点,计算函数值,判断点与直线的位置关系再确定平面区域,而符号判别法只需由A(或B)的符号与不等式的符号的异同直接确定平面区域,相比之下显得快速准确、实用. 2、巧妙简捷地求方程含有参数的直线与已知线段相交时参数的取值范围. 例2:直线 分析:这是一道一题多解的好题,但有的解法运算量大,有的解法容易出错,若用命题2的结论可轻而易举地得出正确结果,解法如下: 解:设 直线 练习题: 1、表示图中阴影部分的平面区域内的点(x,y)所满足的约束件是_________. 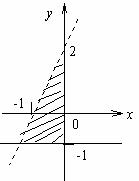 2、直线 答案:1、 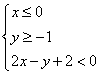 2、 2、(责任编辑:admin) |
