|
数列中的数学思想 丁赛军 在数列综合问题中蕴含着许我重要的数学思想，如归纳思想、函数思想、方程思想、递推思想、化归思想、分类讨论思想，在这些思想的指导下产生许多解决数列问题的方法，让学生充分理解和掌握这些思想和方法，对提高解决数列综合问题的能力很为重要。 一. 归纳思想 通过对命题在特殊情况下的考察与探索，发现并归纳出一般性的结论，再运用数学的方法对结论进行证明，这种归纳思想形成了解决数列问题的一种重要方法；观察、归纳、猜想、证明。 例1. 设  是数列 的前n项和，且 ，数列 的通项公式为 ，将数列和的公共项按它们在原数列中的先后顺序排成一个新数列 ，求 。分析：由  ，得 ，直接求出它们的公共项比较困难，可列举它们开始的若干项进行观察，发现规律后再进行证明。解：   ，727，……，2187，……。猜想：  ，……是公共项，即 。证明：若  是公共项，则存在 ，使得 。那么   这说明当 是公共项时， 不是公共项， 是公共项， 。二. 方程思想 在等差与等比数列中，常常需要研究  之间关系，我们可以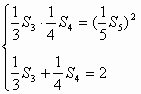以方程思想为指导，寻找未知数个数与方程个数间的关系。例2. 设 是等差数列的前n项和，已知 与 的等比中项为 ，与的等差中项为1，求。解：由题意知  即 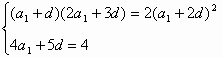 解得 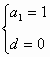 或  或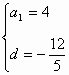 三. 递推思想 在数列问题中，学生往往很重视通项，但有时用递推关系给出数列比通项更简洁，这就要求培养学生的递推思想。 例3. 某林场原有森林木材量a，木材以每年25%的增长率生成，而每年要砍伐的木材量为x，为使经过20年木材存有量翻两番，求每年砍伐量x（  ）分析：设经过n年后木材量为 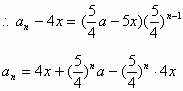，则根据题意有 即  其中  于是数列  是首项为 ，公比为 的等比数列， 由题意知 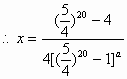 时，  设    四. 函数思想 数列是特殊的函数，因而许多数列问题的讨论可用函数方法解决。 例4. 在xOy平面上有一点列  ，……，对每个自然数n，点 位于函数 的图象上，且点、点 与点 构成一个以为顶点的等腰三角形。（1）求点 的纵坐标 的表达式；（2）若对每个自然数n，以  为边长能构成一个三角形，求a的取值范围。分析：（1）由点 、点（n，0）与点构成以为顶点的等腰三角形，知 。又  点在函数 的图象上 （2）   函数是减函数对每个自然数n都有 则以 为边长能构成三角形的充要条件是 即  解得  或  五. 分类讨论思想 数列中许多问题在不同的情形下可得到不同的结论，这时往往需分类讨论。 例5. 3个实数  ， 适当排列，分别取常用对数后构成公差为1的等差数列，求此时a的值。分析：此题关键是3个数以怎样的顺序构成等差数列？由公差为1可知，所成等差数列一定是递增的，所以需判断这3个数的大小关系，从而减少分类次数。 解：记   由题意知   解得  考虑差      又  （1）当 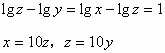 时， （不舍题意）（2）当  时， ，此时有  构成公差为1的等差数列，即 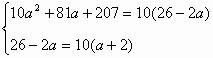即  解得  （3）当  时， ，此时  构成公差为1的等差数列，即   上述方程组无解，即a不存在。 综合（1）（2）（3）知 (责任编辑：admin) |