|
数值比较中数学思想方法例话 山东省临清市第二中学 马英济 数学思想方法是从数学内容中提炼出来的数学知识的精髓，是知识转化为能力的桥梁，有着普遍应用的意义.“变则通”化归思想首当其冲. 【题目1】：比较1618与1816的大小. 思路1：  思路2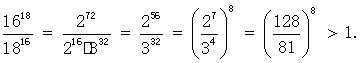：  ∴ 1618 > 1816 . [评说]：比较法是证明不等式的最基本的方法，具体的有作差比较和作商比较两种.其基本思想是把难以比较的式子变成“其差”与“0”比较大小或“其商”与“1”比较大小.当两多项式的值比较时，常用作差比较，当两式是乘积形式（或幂指数式）时，常用作商比较.整个过程体现着转化与化归思想. 【题目2】： 若  则A. a<b<c B. c<b<a C. c<a<b D. b<a<c 解法一、看结构，化同底、同次根式；找关系，利用函数单调性. 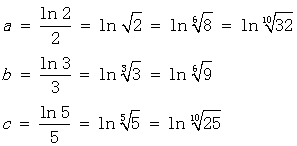 ∵ 8<9 , ∴ a<b . ∵ 25<32 , ∴c<a . 综上 c<a<b . 故选C. 解法二、作差比较，基本方法是参考  ∴ a<b.  ∴ c<a.  ∴ a<b. 综上 c<a<b . 故选C. 解法三、数形结合，考虑直线斜率公式 作出函数y=  的图象，设A(2,ln2),B(3,ln3),C(5,ln5). 则  (K表示斜率)，作出OA,OB,OC,观察知 ，即c<a<b.【点评】数形结合的重点是研究“以形助数”和“以数定形”，华罗庚教授曾言“数形结合百般好，隔裂分家万事休.”“数形结合”数是基础，是关键，既要“以形助数”又要“以数定形”.借助于图象研究函数的性质是一种常用的方法，函数图象的几何特征与数量特征紧密结合，体现了数形结合的思想方法，运用这种数形结合的思想方法有助于探求解题思路，提高解题思路，检验解题结果. 解法四、以导数为工具，利用函数思想解答，凸显单调性法  构造函数 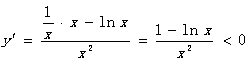 ,  , ∴ 函数  在（e,+∞）上是减函数.∴ f(3)>f(4)>f(5),即  ，故c<a<b. 【点评】结合本题的特点，可考虑构造一个辅助函数 运用函数的性质去分析问题，转化问题.单调性法，就是利用函数的重要性质（单调性）寻求问题的突破与解决.对有些数学问题，若能与函数单调性联系起来，常能获得简捷、轻松、直观的解决.[评说]此题是常规的自然对数，可是它的思想方法并不平常.解法一是运用化规思想，结合对数函数的性质解答；解法二是比较法中的比差法，结合对数函数的性质解答；解法三是利用数形结合思想，联想直线的斜率公式，解答直观形象；解法四结合函数思想，以导数为工具，利用函数单调性求解.“结识新朋友，不忘老朋友”，通往罗马，道路条条能走. 【题目3】：比较  的大小.尝试一：  ，两边取常用对数，得  ，即  ，两边平方，得  ∵  ∴  ， ∴  ，即 .【点评】“均值不等式”，比较大小可尝试.利用基本不等式及其变形，解题方便灵活，简单易行.如  （当且仅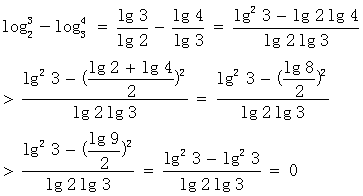当a=b取等号）; 在本题中做到了巧妙的应用.尝试二：  .∴ 【点评】作差通分，防缩技巧“现身”.“防缩法”是式子适当放大与缩小，技巧性强，应用广泛.经常采用的技巧是⑴舍去一些正项（或负项），⑵在积或和中换大（或换小）某些项，⑶扩大（或缩小）分式的分子（或分母）等. 尝试三：  ∴ .【点评】同上. 尝试四： 探究：函数 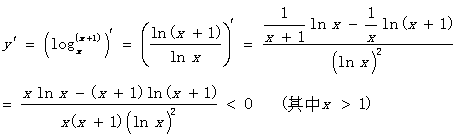 的单调性 ∴ 函数  在（1，+∞）上是减函数.∴f(2)>f(3) .即 .思考与体会：  [评说]“综合”、“作商”、“作差”，解题始终不忘“老法”.尝试一二三，“基本不等式”闯难关.导数工具出现，解决问题一大片.导数的引入，我们解题的视野与思路又拓宽了一大步. “思想方法千般好，化归转化离不了”所谓转化与化归思想，就是研究和解决有关数学问题时采用某种手段，将问题通过变换使之转化归结为在已知知识范围内可以解决的一种方法.一般总是将复杂的问题通过变换转化为简单的问题，将较难的问题通过变换转化为容易解决的问题，将未解决的问题变换转化为已解决的问题.我们可以说数学解题就是转化问题，每一个数学问题都是在不断地转化中解决的.即使是数形结合思想、函数方程思想也都是转化与化归思想的表现形式. 转化与化归，解决问题一大堆.化归思想做为高中数学中的基本核心思想理应受到高度重视 , 它在培养数学素养和解题能力方面都起到了很重要的作用 , 化归思想是数学的灵魂 ． (责任编辑：admin) |