|
高中数学竞赛讲义（八） ──平面向量 一、基础知识 定义1 既有大小又有方向的量，称为向量。画图时用有向线段来表示，线段的长度表示向量的模。向量的符号用两个大写字母上面加箭头，或一个小写字母上面加箭头表示。书中用黑体表示向量，如a. |a|表示向量的模，模为零的向量称为零向量，规定零向量的方向是任意的。零向量和零不同，模为1的向量称为单位向量。 定义2 方向相同或相反的向量称为平行向量（或共线向量），规定零向量与任意一个非零向量平行和结合律。 定理1 向量的运算，加法满足平行四边形法规，减法满足三角形法则。加法和减法都满足交换律和结合律。 定理2 非零向量a, b共线的充要条件是存在实数  0，使得a= f定理3 平面向量的基本定理，若平面内的向量a, b不共线，则对同一平面内任意向是c，存在唯一一对实数x, y，使得c=xa+yb，其中a, b称为一组基底。 定义3 向量的坐标，在直角坐标系中，取与x轴，y轴方向相同的两个单位向量i, j作为基底，任取一个向量c，由定理3可知存在唯一一组实数x, y，使得c=xi+yi，则（x, y）叫做c坐标。 定义4 向量的数量积，若非零向量a, b的夹角为  ，则a, b的数量积记作a·b=|a|·|b|cos=|a|·|b|cos<a, b>，也称内积，其中|b|cos叫做b在a上的投影（注：投影可能为负值）。定理4 平面向量的坐标运算：若a=(x1, y1), b=(x2, y2)， 1．a+b=(x1+x2, y1+y2), a-b=(x1-x2, y1-y2)， 2．λa=(λx1, λy1), a·(b+c)=a·b+a·c， 3．a·b=x1x2+y1y2, cos(a, b)= 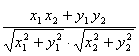 (a, b 0),4. a//b  x1y2=x2y1, a bx1x2+y1y2=0.定义5 若点P是直线P1P2上异于p1，p2的一点，则存在唯一实数λ，使  ，λ叫P分 所成的比，若O为平面内任意一点，则 。由此可得若P1，P，P2的坐标分别为(x1, y1), (x, y), (x2, y2)，则 定义6 设F是坐标平面内的一个图形，将F上所有的点按照向量a=(h, k)的方向，平移|a|=  个单位得到图形 ，这一过程叫做平移。设p(x, y)是F上任意一点，平移到上对应的点为 ，则 称为平移公式。定理5 对于任意向量a=(x1, y1), b=(x2, y2), |a·b|≤|a|·|b|，并且|a+b|≤|a|+|b|. 【证明】 因为|a|2·|b|2-|a·b|2=  -(x1x2+y1y2)2=(x1y2-x2y1)2≥0，又|a·b|≥0, |a|·|b|≥0，所以|a|·|b|≥|a·b|. 由向量的三角形法则及直线段最短定理可得|a+b|≤|a|+|b|. 注：本定理的两个结论均可推广。1）对n维向量，a=(x1, x2,…,xn)，b=(y1, y2, …, yn)，同样有|a·b|≤|a|·|b|，化简即为柯西不等式：  (x1y1+x2y2+…+xnyn)2≥0，又|a·b|≥0, |a|·|b|≥0，所以|a|·|b|≥|a·b|. 由向量的三角形法则及直线段最短定理可得|a+b|≤|a|+|b|. 注：本定理的两个结论均可推广。1）对n维向量，a=(x1, x2,…,xn), b=(y1, y2, …, yn)，同样有|a·b|≤|a|·|b|，化简即为柯西不等式： (x1y1+x2y2+…+xnyn)2。2）对于任意n个向量，a1, a2, …,an，有| a1, a2, …,an|≤| a1|+|a2|+…+|an|。 二、方向与例题 1．向量定义和运算法则的运用。 例1 设O是正n边形A1A2…An的中心，求证：  【证明】 记  ，若 ，则将正n边形绕中心O旋转 后与原正n边形重合，所以 不变，这不可能，所以 例2 给定△ABC，求证：G是△ABC重心的充要条件是  【证明】必要性。如图所示，设各边中点分别为D，E，F，延长AD至P，使DP=GD，则  又因为BC与GP互相平分， 所以BPCG为平行四边形，所以BG  PC，所以 所以  充分性。若  ，延长AG交BC于D，使GP=AG，连结CP，则 因为 ，则 ，所以GBCP，所以AG平分BC。同理BG平分CA。 所以G为重心。 例3 在凸四边形ABCD中，P和Q分别为对角线BD和AC的中点，求证：AB2+BC2+CD2+DA2=AC2+BD2+4PQ2。 【证明】 如图所示，结结BQ，QD。 因为  ，所以  =  · =  ①又因为  同理  ， ② ， ③由①，②，③可得   。得证。 2．证利用定理2证明共线。 例4 △ABC外心为O，垂心为H，重心为G。求证：O，G，H为共线，且OG：GH=1：2。 【证明】 首先  =   其次设BO交外接圆于另一点E，则连结CE后得CE  又AH BC，所以AH//CE。又EA AB，CHAB，所以AHCE为平行四边形。所以  所以  ，所以  ，所以  与 共线，所以O，G，H共线。所以OG：GH=1：2。 3．利用数量积证明垂直。 例5 给定非零向量a, b. 求证：|a+b|=|a-b|的充要条件是a b.【证明】|a+b|=|a-b| (a+b)2=(a-b)2a2+2a·b+b2=a2-2a·b+b2a·b=0ab.例6 已知△ABC内接于⊙O，AB=AC，D为AB中点，E为△ACD重心。求证：OE CD。【证明】 设  ，则  ， 又  ，所以    a·(b-c). （因为|a|2=|b|2=|c|2=|OH|2）又因为AB=AC，OB=OC，所以OA为BC的中垂线。 所以a·(b-c)=0. 所以OE CD。4．向量的坐标运算。 例7 已知四边形ABCD是正方形，BE//AC，AC=CE，EC的延长线交BA的延长线于点F，求证：AF=AE。 【证明】 如图所示，以CD所在的直线为x轴，以C为原点建立直角坐标系，设正方形边长为1，则A，B坐标分别为（-1，1）和（0，1），设E点的坐标为（x, y），则  =(x, y-1),  ，因为 ，所以-x-(y-1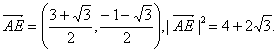)=0.又因为  ，所以x2+y2=2.由①，②解得  所以  设  ，则 。由 和 共线得 所以  ，即F ，所以  =4+ ，所以AF=AE。三、基础训练题 1．以下命题中正确的是__________. ①a=b的充要条件是|a|=|b|，且a//b；②(a·b)·c=(a·c)·b；③若a·b=a·c，则b=c；④若a, b不共线，则xa+yb=ma+nb的充要条件是x=m, y=n；⑤若  ，且a, b共线，则A，B，C，D共线；⑥a=(8, 1)在b=(-3, 4)上的投影为-4。2．已知正六边形ABCDEF，在下列表达式中：①  ；② ；③  ；④ 与 ，相等的有__________.3．已知a=y-x, b=2x-y, |a|=|b|=1, a·b=0，则|x|+|y|=__________. 4．设s, t为非零实数，a, b为单位向量，若|sa+tb|=|ta-sb|，则a和b的夹角为__________. 5．已知a, b不共线，  =a+kb,  =la+b，则“kl-1=0”是“M，N，P共线”的__________条件.6．在△ABC中，M是AC中点，N是AB的三等分点，且  ，BM与CN交于D，若 ，则λ=__________.7．已知  不共线，点C分 所成的比为2， ，则 __________.8．已知  =b, a·b=|a-b|=2，当△AOB面积最大时，a与b的夹角为__________.9．把函数y=2x2-4x+5的图象按向量a平移后得到y=2x2的图象，c=(1, -1), 若  ，c·b=4，则b的坐标为__________.10．将向量a=(2, 1)绕原点按逆时针方向旋转  得到向量b，则b的坐标为__________.11．在Rt△BAC中，已知BC=a，若长为2a的线段PQ以点A为中点，试问  与 的夹角取何值时 的值最大？并求出这个最大值。12．在四边形ABCD中，  ，如果a·b=b·c=c·d=d·a，试判断四边形ABCD的形状。 四、高考水平训练题 1．点O是平面上一定点，A，B，C是此平面上不共线的三个点，动点P满足  则点P的轨迹一定通过△ABC的________心。2．在△ABC中，  ，且a·b<0，则△ABC的形状是__________.3．非零向量  ，若点B关于 所在直线对称的点为B1，则 =__________.4．若O为△ABC 的内心，且  ，则△ABC 的形状为__________.5．设O点在△ABC 内部，且  ，则△AOB与△AOC的面积比为__________.6．P是△ABC所在平面上一点，若  ，则P是△ABC 的__________心.7．已知  ，则||的取值范围是__________.8．已知a=(2, 1), b=(λ, 1)，若a与b的夹角为锐角，则λ的取值范围是__________. 9．在△ABC中，O为中线AM上的一个动点，若AM=2，则  的最小值为__________.10．已知集合M={a|a=(1, 2)+ λ(3, 4), λ∈R}，集合N={a|a=(-2, -2)+ λ(4, 5), λ∈R},mj M  N=__________.11．设G为△ABO的重心，过G的直线与边OA和OB分别交于P和Q，已知  ，△OAB与△OPQ的面积分别为S和T，（1）求y=f(x)的解析式及定义域；（2）求  的取值范围。12．已知两点M（-1，0），N（1，0），有一点P使得  成公差小于零的等差数列。（1）试问点P的轨迹是什么？（2）若点P坐标为(x0, y0), 为 与 的夹角，求tan.五、联赛一试水平训练题 1．在直角坐标系内，O为原点，点A，B坐标分别为（1，0），（0，2），当实数p, q满足  时，若点C，D分别在x轴，y轴上，且 ，则直线CD恒过一个定点，这个定点的坐标为___________.2．p为△ABC内心，角A，B，C所对边长分别为a, b, c. O为平面内任意一点，  则 =___________（用a, b, c, x, y, z表示）.3．已知平面上三个向量a, b, c均为单位向量，且两两的夹角均为1200，若|ka+b+c|>1(k∈R)，则k的取值范围是___________. 4．平面内四点A，B，C，D满足  ，则 的取值有___________个.5．已知A1A2A3A4A5是半径为r的⊙O内接正五边形，P为⊙O上任意一点，则  取值的集合是___________.6．O为△ABC所在平面内一点，A，B，C为△ABC 的角，若sinA· +sinB· +sinC· ，则点O为△ABC 的___________心.7．对于非零向量a, b, “|a|=|b|”是“(a+b) (a-b)”的___________条件.8．在△ABC 中，  ，又(c·b)：(b·a)：(a·c)=1：2：3，则△ABC 三边长之比|a|：|b|：|c|=____________.9．已知P为△ABC内一点，且  ，CP交AB于D，求证： 10．已知△ABC的垂心为H，△HBC，△HCA，△HAB的外心分别为O1，O2，O3，令  ，求证：（1）2p=b+c-a；（2）H为△O1O2O3的外心。11．设坐标平面上全部向量的集合为V，a=(a1, a2)为V中的一个单位向量，已知从V到  的变换T，由T(x)=-x+2(x·a)a(x∈V)确定，（1）对于V的任意两个向量x, y, 求证：T(x)·T(y)=x·y； （2）对于V的任意向量x，计算T[T(x)]-x； （3）设u=(1, 0)；  ，若 ，求a.六、联赛二试水平训练题 1．已知A，B为两条定直线AX，BY上的定点，P和R为射线AX上两点，Q和S为射线BY上的两点，  为定比，M，N，T分别为线段AB，PQ，RS上的点， 为另一定比，试问M，N，T三点的位置关系如何？证明你的结论。2．已知AC，CE是正六边形ABCDEF的两条对角线，点M，N分别内分AC，CE，使得AM：AC=CN：CE=r，如果B，M，N三点共线，求r. 3．在矩形ABCD的外接圆的弧AB上取一个不同于顶点A，B的点M，点P，Q，R，S是M分别在直线AD，AB，BC，CD上的射影，求证：直线PQ与RS互相垂直。 4．在△ABC内，设D及E是BC的三等分点，D在B和F之间，F是AC的中点，G是AB的中点，又设H是线段EG和DF的交点，求比值EH：HG。 5．是否存在四个平面向量，两两不共线，其中任何两个向量之和均与其余两个向量之和垂直？ 6．已知点O在凸多边形A1A2…An内，考虑所有的  AiOAj，这里的i, j为1至n中不同的自然数，求证：其中至少有n-1个不是锐角。7．如图，在△ABC中，O为外心，三条高AD，BE，CF交于点H，直线ED和AB交于点M，FD和AC交于点N，求证：（1）OB DF，OCDE，（2）OHMN。8．平面上两个正三角形△A1B1C1和△A2B2C2，字母排列顺序一致，过平面上一点O作  ，求证△ABC为正三角形。9．在平面上给出和为  的向量a, b, c, d，任何两个不共线，求证：|a|+|b|+|c|+|d|≥|a+d|+|b+d|+|c+d|. 本系列讲座由在人教中数论坛网友“0.1”整理提供，感谢他（她）的分享。 (责任编辑：admin) |